题目内容
【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,且BC=2AF。
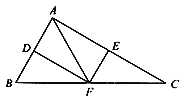
(1)求证:四边形ADEF为矩形;
(2)若∠C=30°、AF=2,写出矩形ADEF的周长。
【答案】(1)证明见解析 (2)![]()
【解析】
(1)连接DE.根据三角形的中位线的性质即可得到结论;
(2)根据矩形的性质得到∠BAC=∠FEC=90°,解直角三角形即可得到结论.
(1)连接DE,
∵E、F分别是AC,BC中点
∴EF//AB,EF=![]() AB
AB
∵点D是AB中点
∴AD=![]() AB,AD=EF
AB,AD=EF
∴四边形ADFE为平行四边形
∵点D、E分别为AB、AC中点
∴DE=![]() BC,
BC,
∵BC=2AF
∴DE=AF
∴四边形ADEF为矩形.
(2)∵四边形ADFE是矩形,
∴∠BAC=∠FEC=90°,
∵AF=2,F为BC中点,
∴BC=4,CF=2,
∵∠C=30°
∴AC=![]() ,CE=
,CE=![]() ,EF=1,
,EF=1,
∴AE=![]()
∴矩形ADEF的周长为![]() ;
;

练习册系列答案
相关题目