题目内容
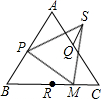 已知:如图,正三角形ABC中,P为AB的中点,Q为AC的中点,R为BC 的中点,M为RC上任意一点,△PMS为正三角形.求证:RM=QS.
已知:如图,正三角形ABC中,P为AB的中点,Q为AC的中点,R为BC 的中点,M为RC上任意一点,△PMS为正三角形.求证:RM=QS.
分析:连接PR、PQ,根据P、Q、R为中点,根据三角形中位线定理可得PQ=PR,利用60°证明∠QPS=∠RPN,再根据△PMS为正三角形可得PS=PM,然后利用边角边定理证明△PRM与△PQS全等,再根据全等三角形对应边相等即可证明.
解答: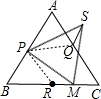 证明:连接PR、PQ,∵P为AB的中点,Q为AC的中点,R为BC 的中点,
证明:连接PR、PQ,∵P为AB的中点,Q为AC的中点,R为BC 的中点,
∴PQ=
BC,PR=
AC,
∴PQ=PR,
∵∠APQ=∠BPR=60°,
∴∠RPQ=180°-2×60°=60°,
又∵∠QPS=∠MPS-∠MPQ=60°-∠MPQ,
∠RPM=∠RPQ-∠MPQ=60°-∠MPQ,
∴∠QPS=∠RPM,
在△PRM与△PQS中,
,
∴△PRM≌△PQS(SAS).
∴RM=QS.
 证明:连接PR、PQ,∵P为AB的中点,Q为AC的中点,R为BC 的中点,
证明:连接PR、PQ,∵P为AB的中点,Q为AC的中点,R为BC 的中点,∴PQ=
| 1 |
| 2 |
| 1 |
| 2 |
∴PQ=PR,
∵∠APQ=∠BPR=60°,
∴∠RPQ=180°-2×60°=60°,
又∵∠QPS=∠MPS-∠MPQ=60°-∠MPQ,
∠RPM=∠RPQ-∠MPQ=60°-∠MPQ,
∴∠QPS=∠RPM,
在△PRM与△PQS中,
|
∴△PRM≌△PQS(SAS).
∴RM=QS.
点评:本题主要考查了等边三角形的三条边都相等,每一个角都是60°的性质,三角形的中位线定理,全等三角形的判定与性质,利用全等三角形证明线段相等是常用的方法,需要熟练掌握.

练习册系列答案
相关题目
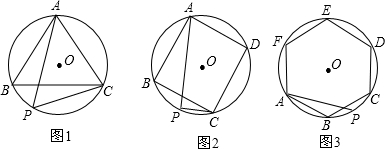
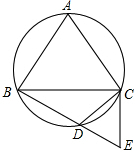 已知:如图,△ABC是⊙O的内接正三角形,点D是
已知:如图,△ABC是⊙O的内接正三角形,点D是
 已知:如图,正三角形ABC中,P为AB的中点,Q为AC的中点,R为BC 的中点,M为RC上任意一点,△PMS为正三角形.求证:RM=QS.
已知:如图,正三角形ABC中,P为AB的中点,Q为AC的中点,R为BC 的中点,M为RC上任意一点,△PMS为正三角形.求证:RM=QS.