题目内容
(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为弧BC上一动点,求证:PA=PB+PC;(2)如图2,四边形ABCD是⊙O的内接正方形,点P为弧BC上一动点,求证:PA=PC+
| 2 |
(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为弧BC上一动点,请探究PA、PB、PC三者之间有何数量关系,并给予证明.
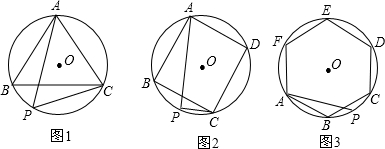
分析:(1)延长BP至E,使PE=PC,连接CE,证明△PCE是等边三角形.利用CE=PC,∠E=∠3=60°,∠EBC=∠PAC,得到△BEC≌△APC,所以PA=BE=PB+PC;
(2)过点B作BE⊥PB交PA于E,证明△ABE≌△CBP,所以PC=AE,可得PA=PC+
PB.
(3)在AP上截取AQ=PC,连接BQ可证△ABQ≌△CBP,所以BQ=BP.又因为∠APB=30°.所以PQ=
PB,PA=PQ+AQ=
PB+PC.
(2)过点B作BE⊥PB交PA于E,证明△ABE≌△CBP,所以PC=AE,可得PA=PC+
| 2 |
(3)在AP上截取AQ=PC,连接BQ可证△ABQ≌△CBP,所以BQ=BP.又因为∠APB=30°.所以PQ=
| 3 |
| 3 |
解答: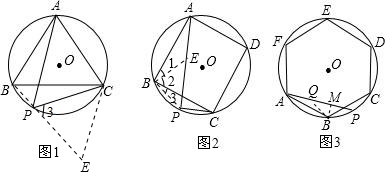 证明:(1)延长BP至E,使PE=PC,
证明:(1)延长BP至E,使PE=PC,
连接CE.∵A、B、P、C四点共圆,
∴∠BAC+∠BPC=180°,
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP,
∵△ABC、△ECP为等边三角形,
∴CE=PC,AC=BC,
∴△BEC≌△APC(SAS),
∴PA=BE=PB+PC.(2分)
(2)过点B作BE⊥PB交PA于E.
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
又∵∠APB=45°,
∴BP=BE,∴PE=
PB;
又∵AB=BC,
∴△ABE≌△CBP,
∴PC=AE.
∴PA=AE+PE=PC+
PB.(4分)
(3)答:PA=PC+
PB;
证明:过点B,作BM⊥AP,在AP上截取AQ=PC,
连接BQ,∵∠BAP=∠BCP,AB=BC,
∴△ABQ≌△CBP,
∴BQ=BP.
∴MP=QM,
又∵∠APB=30°,
∴cos30°=
,
∴PM=
PB,
∴PQ=
PB
∴PA=PQ+AQ=
PB+PC(7分)
 证明:(1)延长BP至E,使PE=PC,
证明:(1)延长BP至E,使PE=PC,连接CE.∵A、B、P、C四点共圆,
∴∠BAC+∠BPC=180°,
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP,
∵△ABC、△ECP为等边三角形,
∴CE=PC,AC=BC,
∴△BEC≌△APC(SAS),
∴PA=BE=PB+PC.(2分)
(2)过点B作BE⊥PB交PA于E.
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
又∵∠APB=45°,
∴BP=BE,∴PE=
| 2 |
又∵AB=BC,
∴△ABE≌△CBP,
∴PC=AE.
∴PA=AE+PE=PC+
| 2 |
(3)答:PA=PC+
| 3 |
证明:过点B,作BM⊥AP,在AP上截取AQ=PC,
连接BQ,∵∠BAP=∠BCP,AB=BC,
∴△ABQ≌△CBP,
∴BQ=BP.
∴MP=QM,
又∵∠APB=30°,
∴cos30°=
| PM |
| BP |
∴PM=
| ||
| 2 |
∴PQ=
| 3 |
∴PA=PQ+AQ=
| 3 |
点评:本题考查三角形全等的性质和判定方法以及正多边形和圆的有关知识.要熟悉这些基本性质才能灵活运用解决综合性的习题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上. 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为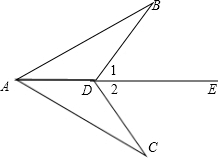 已知,如图,∠1=∠2,
已知,如图,∠1=∠2, 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为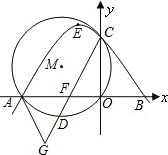 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧