题目内容
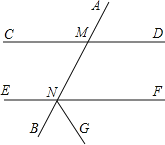
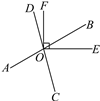
【题目】如图,直线AB,CD相交于点O,OE⊥AB,OF⊥CD.
(1)若OC恰好是∠AOE的平分线,则OA是∠COF的平分线吗?请说明理由;
(2)若∠EOF=5∠BOD,求∠COE的度数.

【答案】(1)OA是∠COF的平分线;(2)∠COE=60°
【解析】
(1)利用角平分线的性质和垂直的定义易得∠AOC=![]() ∠AOE=45°,再由OF⊥CD,可得∠COF=90°,易得∠AOF,由垂直的定义可得结论;
∠AOE=45°,再由OF⊥CD,可得∠COF=90°,易得∠AOF,由垂直的定义可得结论;
(2)设∠AOC=x,易得∠BOD=x,可得∠COE=90°-x,∠EOF=180°-x,利用∠EOF=5∠BOD,解得x,可得∠COE.
(1)OA是∠COF的平分线.
∵OE⊥AB,
∴∠AOE=90°,
∵OC恰好是∠AOE的平分线,
∴∠AOC=![]() ∠AOE=45°,
∠AOE=45°,
∵OF⊥CD,
∴∠COF=90°,
∴∠AOF=∠COF-∠AOC=90°-45°=45°,
∴OA是∠COF的平分线;
(2)设∠AOC=x,
∴∠BOD=x,
∵∠AOE=90°,
∴∠COE=∠AOE-∠AOC=90°-x,
∴∠EOF=∠COE+∠COF=90°-x+90°=180°-x,
∵∠EOF=5∠BOD,
∴180°-x=5x,
解得x=30,
∴∠COE=90°-30°=60°.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目