题目内容
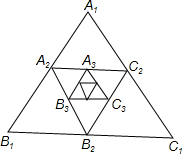 如图,三角形A1B1C1的周长为16,△A1B1C1的三条中位线组成△A2B2C2,△A2B2C2的三条中位线又组成△A3B3C3,…以此类推,得到△AnBnCn,则第4个三角形的周长是
如图,三角形A1B1C1的周长为16,△A1B1C1的三条中位线组成△A2B2C2,△A2B2C2的三条中位线又组成△A3B3C3,…以此类推,得到△AnBnCn,则第4个三角形的周长是分析:根据三角形的中位线平行于第三边且等于第三边的一半,可得后一个三角形的周长等于前一个三角形的周长的一半,根据此规律进行解答.
解答:解:∵△A1B1C1的周长为16,连接AB,BC,CA各边的中点得△A2B2C2,
∴△A2B2C2的周长=
△A1B1C1的周长=
×16=8,
同理:△A3B3C3的周长=
△A2B2C2的周长=
×8=4,
…
以此类推,△AnBnCn的周长=
△An-1Bn-1Cn-1的周长=
×16.
∴第4个三角形的周长是:
×16=
×16=1.
故答案为:1.
∴△A2B2C2的周长=
| 1 |
| 2 |
| 1 |
| 2 |
同理:△A3B3C3的周长=
| 1 |
| 2 |
| 1 |
| 2 |
…
以此类推,△AnBnCn的周长=
| 1 |
| 2 |
| 1 |
| 2n |
∴第4个三角形的周长是:
| 1 |
| 2n |
| 1 |
| 24 |
故答案为:1.
点评:此题考查了三角形的中位线定理,推出后一个三角形的周长等于前一个三角形周长的一半是解题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
 如图,在Rt△ABC中,AB=3,BC=4,∠ABC=90°,过B作BA1⊥AC,过A1作A1B1⊥BC,得阴影Rt△A1B1B;再过B1作B1A2⊥AC,过A2作A2B2⊥BC,得阴影Rt△A2B2B1;…如此下去,请猜测这样得到的所有阴影三角形的面积之和为( )
如图,在Rt△ABC中,AB=3,BC=4,∠ABC=90°,过B作BA1⊥AC,过A1作A1B1⊥BC,得阴影Rt△A1B1B;再过B1作B1A2⊥AC,过A2作A2B2⊥BC,得阴影Rt△A2B2B1;…如此下去,请猜测这样得到的所有阴影三角形的面积之和为( )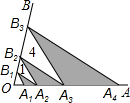 如图,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3.若△A2B1B2,△A3B2B3的面积分别为1,4,则图中三个阴影三角形面积之和为
如图,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3.若△A2B1B2,△A3B2B3的面积分别为1,4,则图中三个阴影三角形面积之和为 10、如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2010,最少经过_____次操作( )
10、如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2010,最少经过_____次操作( )
