题目内容
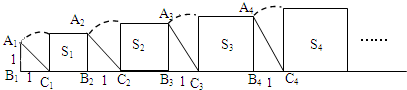
观察如图所包含规律(图中三角形均是直角三角形,且一条直角边始终为1,四边形均为正方形.S1,S2,S3,…Sn依次表示正方形的面积,每个正方形边长与它左边相邻的直角三角形斜边相等),再回答下列问题.
(1)填表:
(2)当s1+s2+s3+s4+…+sn=465时,求n.

(1)填表:
| 直角边 | A1B1 | A2B2 | A3B3 | A4B4 | … | AnBn |
| 长度 | 1 | … |

分析:(1)结合图示,根据勾股定理直接计算即可;
(2)根据正方形的边长,算出每个小正方形的面积,观察发现是一个等差数列,根据等差数列和的计算公式,可得到一个一元二次方程,解方程可得到n的值.
(2)根据正方形的边长,算出每个小正方形的面积,观察发现是一个等差数列,根据等差数列和的计算公式,可得到一个一元二次方程,解方程可得到n的值.
解答:解:(1)A1B1=
=
;A2B2=
=
;A3B3=
=
=2;…由此可以推断出:AnBn=
;
(2)S1=(
)2=2,
S2=(
)2=3,
S3=22=4,
S4=(
)2=5,
…
Sn=(
)2=n+1;
由s1+s2+s3+s4+…+sn=465可得:
2+3+4+5+…+n+1=465,
1+2+3+4+5+…+n=465,
有等差数列公式可知:
=465,
解得:n=-31(不合题意舍去)或n=30,
故:n=30.
| 12+12 |
| 2 |
(
|
| 3 |
(
|
| 4 |
| n |
| 直角边 | A1B1 | A2B2 | A3B3 | A4B4 | … | AnBn | ||||||
| 长度 | 1 |
|
|
2 | … |
|
| 2 |
S2=(
| 3 |
S3=22=4,
S4=(
| 5 |
…
Sn=(
| n+1 |
由s1+s2+s3+s4+…+sn=465可得:
2+3+4+5+…+n+1=465,
1+2+3+4+5+…+n=465,
有等差数列公式可知:
| n(n+1) |
| 2 |
解得:n=-31(不合题意舍去)或n=30,
故:n=30.
点评:此题主要考查了勾股定理,关键是熟练把握勾股定理公式a2+b2=c2,此题中的难点是根据正方形的面积和求n的值,此题要用到等差数列和的计算公式.

练习册系列答案
相关题目
观察如图所包含规律(图中三角形均是直角三角形,且一条直角边始终为1,四边形均为正方形.S1,S2,S3,…Sn依次表示正方形的面积,每个正方形边长与它左边相邻的直角三角形斜边相等),再回答下列问题.
(1)填表:
| 直角边 | A1B1 | A2B2 | A3B3 | A4B4 | … | AnBn |
| 长度 | 1 | … |