题目内容
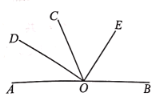
【题目】如图,已知在△ABC中,D为BC的中点,连接AD,E为AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:四边形ADCF为平行四边形.
(2)当四边形ADCF为矩形时,AB与AC应满足怎样的数量关系?请说明理由.
【答案】(1)详见解析;(2)四边形ADCF为矩形时AB=AC,理由详见解析.
【解析】
(1)利用△AEF≌△DEB得到AF=DB,所以AF=DC,根据一组对边平行且相等的四边形是平行四边形可证明四边形ADCF为平行四边形;
(2)利用等腰三角形的性质以及矩形的性质得出即可.
(1)∵AF∥BC,
∴∠FAE=∠EDB,∠AFE=∠EBD.
又∵AE=ED,
∴△AEF≌△DEB(AAS),
∴AF=DB,
又∵BD=DC,
∴AF=DC,
∴四边形ADCF为平行四边形;
(2)四边形ADCF为矩形时AB=AC;
理由:∵四边形ADCF为矩形,
∴AD⊥BC,
∴∠ADC=90°,
∵D为BC的中点,
∴AB=AC,
∴四边形ADCF为矩形时AB=AC.

【题目】三位老师周末到某家电专卖店购买冰箱和空调,正值该专卖店举行“迎新春、大优惠”活动,具体优惠情况如下表:
购物总金额(原价) | 折扣率 |
不超过3000元的部分 | 九折 |
超过3000元但不超过5000元的部分 | 八折 |
超过5000元的部分 | 七折 |
(1)李老师所购物品的原价是6000元,李老师实际付 元
(2)已知张老师购买了两件物品(一个冰箱和一个空调)共付费4060元.请问这两件物品的原价总共是多少元?
(3)碰巧同一天赵老师也在同一家专卖店购买了同样的两件物品.但赵老师上午去购买的冰箱,下 午去购买的空调,如此一来赵老师两次付款总额比张老师多花费了140元.已知此冰箱的原价比空调的原价要贵,求这两件物品的原价分别为多少元?