题目内容
 如图,OD=OC,BD=AC,∠O=70度,∠C=30度,则∠BED等于
如图,OD=OC,BD=AC,∠O=70度,∠C=30度,则∠BED等于
- A.45度
- B.50度
- C.55度
- D.60度
B
分析:在△OBC中,已知∠O、∠C的度数,易求得∠OBC=80°;而∠OBC是△BED的外角,欲求∠BED的度数,需先求出∠D的度数;可通过证△OBC≌△OAD,得∠D=∠C,再由∠BED=∠OBC-∠D,得出所求的结论.
解答: 解:∵OD=OC,BD=AC,
解:∵OD=OC,BD=AC,
∴OA=OB,又∠O=∠O,OD=OC,
∴△OAD≌△OBC,(SAS)
∴∠D=∠C=30°,
△OBC中,∠OBC=180°-∠O-∠C=80°,
∴∠BED=∠OBC-∠D=80°-30°=50°.
故选B.
点评:本题主要考查全等三角形的判定和性质以及三角形的外角性质.能够通过全等三角形来求得∠D的度数,是解答此题的关键.
分析:在△OBC中,已知∠O、∠C的度数,易求得∠OBC=80°;而∠OBC是△BED的外角,欲求∠BED的度数,需先求出∠D的度数;可通过证△OBC≌△OAD,得∠D=∠C,再由∠BED=∠OBC-∠D,得出所求的结论.
解答:
 解:∵OD=OC,BD=AC,
解:∵OD=OC,BD=AC,∴OA=OB,又∠O=∠O,OD=OC,
∴△OAD≌△OBC,(SAS)
∴∠D=∠C=30°,
△OBC中,∠OBC=180°-∠O-∠C=80°,
∴∠BED=∠OBC-∠D=80°-30°=50°.
故选B.
点评:本题主要考查全等三角形的判定和性质以及三角形的外角性质.能够通过全等三角形来求得∠D的度数,是解答此题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 9、如图,OD=OC,BD=AC,∠O=70度,∠C=30度,则∠BED等于( )
9、如图,OD=OC,BD=AC,∠O=70度,∠C=30度,则∠BED等于( ) 19、已知:如图,OD=OC,OA=OB.求证:AD=CB.
19、已知:如图,OD=OC,OA=OB.求证:AD=CB. 6、已知:如图,OD=OC,要使△OAD≌△OBC,不能添加的条件是( )
6、已知:如图,OD=OC,要使△OAD≌△OBC,不能添加的条件是( )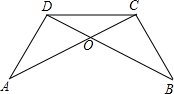 已知:如图,OD=OC,OA=OB.求证:AD=CB.
已知:如图,OD=OC,OA=OB.求证:AD=CB.