题目内容
两个全等的直角三角形ABC和DEF重叠在一起,其中AB=2,AC=1..固定△ABC不动,将△DEF进行如下操作:
小题1:如图(1),△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,它的面积是否变化,如果不变请求出 其面积.如果变化,说明理由.
小题2:如图(2),当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明 理由.
小题1:如图(1),△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,它的面积是否变化,如果不变请求出 其面积.如果变化,说明理由.
小题2:如图(2),当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明 理由.

小题1:根据平移的性质得到:AD=CF=BE.CF∥BD.
∴平行四边形ACFD与平行四边形BCFE的底边相等,且高相等,
∴平行四边形ACFD的面积等于平行四边形BCFE的面积,
又CD与BF分别为两平行四边形的对角线,
∴三角形ACD的面积等于三角形FCD的面积等于三角形CFB的面积等于三角形EFB的面积,
所以三角形ACD的面积等于三角形BEF的面积.
所以S梯形CDBF=S△ABC=
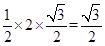 ;
;小题2:在直角三角形ABC中,AD=BD,则CD=BD,
根据平移的性质,得CF=BD,CD=BF,
∴CD=BD=CF=BF,
∴四边形CDBF是菱形.
(1)根据平移的性质,可得AD=BE,CF∥BD.所以三角形ACD的面积等于三角形BEF的面积,则梯形的面积就等于直角三角形ABC的面积;
(2)根据直角三角形一边上的中线等于斜边的一半,以及平移的性质可以证明该四边形的四条边相等,则该四边形是菱形.

练习册系列答案
相关题目
 为对称轴作△ABC的轴对称图形△
为对称轴作△ABC的轴对称图形△ ;
;




 ,该号码实际是 .
,该号码实际是 . 的坐标分别为
的坐标分别为 ,将
,将 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转 得到
得到 .
. 的坐标;
的坐标; 所经过的路径
所经过的路径 的长度.(结果保留
的长度.(结果保留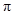 )
)
 时,求CH的长。
时,求CH的长。