题目内容
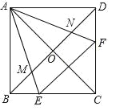
【题目】定义：如图1，抛物线
与x轴交于A，B两点，点P在该抛物线上(P点与A． B两点不重合)，如果△ABP中PA与PB两条边的三边满足其中一边是另一边
倍，则称点P为抛物线的“好”点．
（1）命题：P(0，3)是抛物线
的“好”点．该命题是_____（ 真或假）命题．
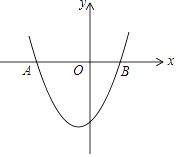
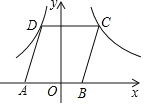
（2）如图2，已知抛物线C:
与
轴交于A，B两点，点P(1，2)是抛物线C的“好”点，求抛物线C的函数表达式．
（3）在（2）的条件下，点Q在抛物线C上，求满足条件S△ABQ=S△ABP的Q点(异于点P)的坐标．
【答案】（1）假；（2）
；（3）
，
．
【解析】
（1）
，则
或
，即点
、
的坐标分别为：
、
，即可求解；
（2）分
、
两种情况，分别求解即可；
（3）
，则点
、
关于抛物线对称轴对称，即可求解．
解：（1）令，则或，即点、的坐标分别为：、，
则
，
，
则
与
两条边满足其中一边是另一边的
倍，则该命题是假命题，
故答案为：假；
（2）将点的坐标代入抛物线表达式得：
，
点
，则点
，
，点
，
则
，
，
①当时，
即
，解得：方程无解；
②当时，
，
解得：
，则
，
故抛物线的表达式为：；
（3），则点、关于抛物线对称轴对称，
函数的对称轴为：
，
则点的坐标为：，．
练习册系列答案
口算能手系列答案
相关题目
