题目内容
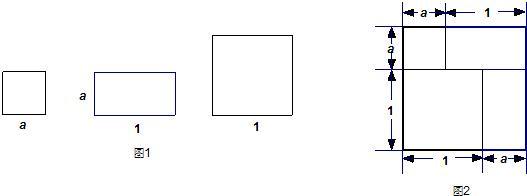
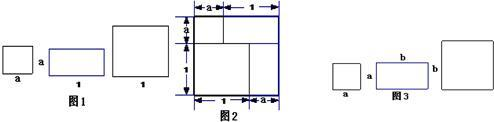
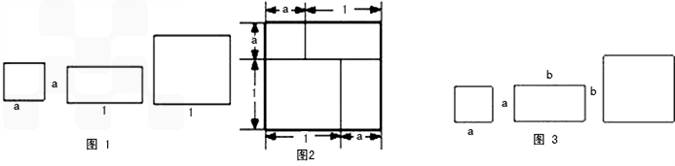
(1)有若干块长方形和正方形硬纸片如图1所示.用若干块这样的硬纸片拼成一个新的长方形,如图2.
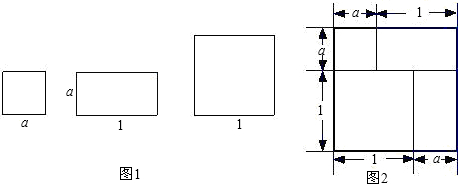
①用两种不同的方法,计算图2中长方形的面积;
②我们知道:同一个长方形的面积是确定的数值.
由此,你可以得出的一个等式为:______.
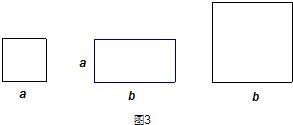
(2)有若干块长方形和正方形硬纸片如图3所示.请你用拼图等方法推出一个完全平方公式,画出你的拼图并说明推出的过程.

解:(1)①长方形的面积=(a+1)×(a+1)=(a+1)2或a2+2a+1,
②(a+1)2=a2+2a+1;
(2)如下图,
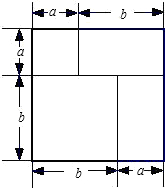
把该长方形视为一个边长为a+b的正方形时,其面积为(a+b)2;
该长方形可视为四个长方形的拼图.四个长方形指两个边长分别为a和b的正方形,以及两个相同的小长方形(长和宽分别为a和b).此时,其面积为a2+2ab+b2,由此,可推导出(a+b)2=a2+2ab+b2.
分析:根据长方形的面积公式=长乘以宽,长方形的长和宽都是a+1,可求出其面积.所拼成的图形的面积等于几个长方形和正方形的面积之和,可以推导出完全平方公式.
点评:解决本题的关键是根据面积公式来求.
②(a+1)2=a2+2a+1;
(2)如下图,

把该长方形视为一个边长为a+b的正方形时,其面积为(a+b)2;
该长方形可视为四个长方形的拼图.四个长方形指两个边长分别为a和b的正方形,以及两个相同的小长方形(长和宽分别为a和b).此时,其面积为a2+2ab+b2,由此,可推导出(a+b)2=a2+2ab+b2.
分析:根据长方形的面积公式=长乘以宽,长方形的长和宽都是a+1,可求出其面积.所拼成的图形的面积等于几个长方形和正方形的面积之和,可以推导出完全平方公式.
点评:解决本题的关键是根据面积公式来求.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目