Question

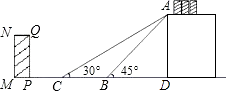
【题目】如图，△ACB和△ECD都是等腰直角三角形，CA=CB，CE=CD，△ACB的顶点A在△ECD的斜边上，若AE=，AD=，则BC的长为______．

Answer 1

【答案】2.

【解析】

由等腰三角形的性质可得AC=BC，DC=EC，∠DCE=∠ACB=90°，∠D=∠CED=45°，可证△ADC≌△BEC，可得AD=BE=，∠D=∠BEC=45°，由勾股定理可求AB=，即可求BC的长．

如图，连接BE，

∵△ACB和△DCE都是等腰直角三角形

∴AC＝BC，DC＝EC，∠DCE＝∠ACB＝90°，∠D＝∠CED＝45°

∴∠DCA＝∠BCE，且AC＝BC，DC＝EC，

∴△ADC≌△BEC（SAS）

∴AD＝BE＝，∠D＝∠BEC＝45°，

∴∠AEB＝90°

∴AB＝＝2

∵AB＝BC

∴BC＝2

故答案为：2.