题目内容
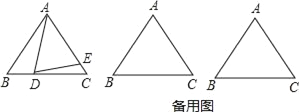
【题目】已知
的内切圆⊙O与AB、BC、AC分别相切于D、E、F，若
，如图1.
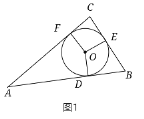
（1）判断的形状，并证明你的结论；
（2）连接AE，若
，求AE的长.
【答案】（1）
为等腰三角形，见解析；（2）
【解析】
（1）根据圆心角和弧的关系、切线的性质和四边形的内角和易证得：
，
，
，进一步即可进行判断；
（2）先根据切线长定理和（1）题的结论得出CE＝BE，再由等腰三角形的性质可得AE⊥BC，然后由OE⊥BC说明A、O、E三点共线，再根据勾股定理即可求出结果.
解：（1）为等腰三角形.
证明：
的内切圆⊙O与AB、BC、AC分别相切于D、E、F，
，
四边形内角和是
，
，，
∵
，
，
，∴
，
为等腰三角形；
（2）∵的内切圆⊙O与AB、BC、AC分别相切于D、E、F，
∴AF=AD，CE=CF，BD=BE，
∵AC＝AB，∴CF=BD，∴CE＝BE，
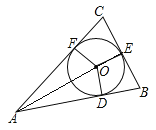
连接AE，如图，∴AE⊥BC，
又∵OE⊥BC，
∴AE过圆心O，
∵
，
∴FC=CE=2，AC=6，
在直角△ACE中，由勾股定理得
.
练习册系列答案
相关题目
