题目内容
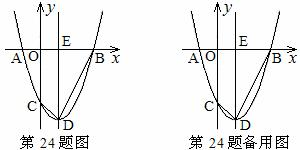
抛物线
与
轴交于A，B两点（点A在点B左侧），与
轴交于点C，点D为顶点。
（1）求点B及点D的坐标；
（2）连结BD，CD，抛物线的对称轴与轴交于点E。
①若线段BD上一点P，使∠DCP=∠BDE，求点P的坐标；
②若抛物线上一点M，作MN⊥CD，交直线CD于点N，使∠CMN=∠BDE，求点M的坐标。
练习册系列答案
相关题目
题目内容
抛物线与轴交于A，B两点（点A在点B左侧），与轴交于点C，点D为顶点。
（1）求点B及点D的坐标；
（2）连结BD，CD，抛物线的对称轴与轴交于点E。
①若线段BD上一点P，使∠DCP=∠BDE，求点P的坐标；
②若抛物线上一点M，作MN⊥CD，交直线CD于点N，使∠CMN=∠BDE，求点M的坐标。
与
轴交于点A和B，与
轴交于点C，点A在
，OB=OC=3。
轴交于A (－4，0) 和B(1，0)两点，与
轴交于C（0，-2）点．
为顶点的抛物线与
轴交于点
．已知
是抛物线上的一点(
、
为正整数)，且它位于对称轴的右侧．若以
、
、
，
是否总成立?请说明理由．
中，抛物线
向左平移1个单位，再向下平移4个单位，得到抛物线
.所得抛物线与
轴交于
两点（点
在点
的左边），与
轴交于点
，顶点为
.
的值；
上是否存在点
，使
与
相似.若存在，求出点