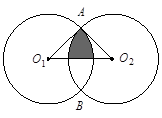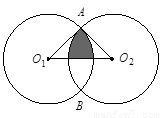题目内容
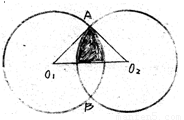
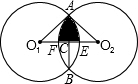
如图,把⊙O1向右平移8个单位长度得⊙O2,两圆相交于A、B,且O1A⊥O2A,则图中阴影部分的面积是
分析:阴影部分的面积=2扇形AO1E的面积-△AO1O2的面积.
解答:解:连接AB交O1O2于点C,
∵把⊙O1向右平移8个单位长度得⊙O2,
∴O1O2=8,
∴O1C=8÷2=4,
易得△AO1O2为等腰直角三角形,
∴AO1=4
,
∴阴影部分的面积=2×
-4
×4
÷2=8π-16,
故答案为8π-16.

∵把⊙O1向右平移8个单位长度得⊙O2,
∴O1O2=8,
∴O1C=8÷2=4,
易得△AO1O2为等腰直角三角形,
∴AO1=4
| 2 |
∴阴影部分的面积=2×
45π(4
| ||
| 360 |
| 2 |
| 2 |
故答案为8π-16.
点评:本题的难点是得到圆的半径,关键是得到阴影的面积的求法.

练习册系列答案
相关题目
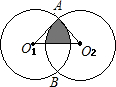 如图,把⊙O1向右平移8个单位长度得⊙O2,两圆相交于A、B,且O1A⊥O2A,则图中阴影部分的面积是( )
如图,把⊙O1向右平移8个单位长度得⊙O2,两圆相交于A、B,且O1A⊥O2A,则图中阴影部分的面积是( )| A、4π-8 | B、8π-16 | C、16π-16 | D、16π-32 |