题目内容

如图，将正方形ABCD以点B为旋转中心顺时针旋转120°得到正方形A′BC′D′，DO⊥C′A′于O，若A′O=数学公式-1，则正方形ABCD的边长为________．


分析：作BE⊥OD于点E，可以设出对角线长是x，则A′F=x，CB可以利用x表示出来，根据OC′=A′C′+A′O，即可得到一个关于x的方程，从而求得对角线长，则边长即可求得．
解答：作BE⊥OD于点E．

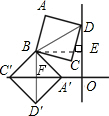
设BD=x，则A′C′=x，A′F=x，
∵BD′⊥OC′，OD⊥OC′，
∴BD′∥OD，
∴∠BDO=180°-∠DBD′=180°-120°=60°，
∴OF=BE=BD•sin∠BDO=x．
即x+（-1）=x，
解得：x=2，
∴边长是：x=．
故答案是：．
点评：本题主要考查了正方形的性质，先作出辅助线转化为解直角三角形，最终转化为方程问题是解题的基本思路．
练习册系列答案
相关题目
探究问题：
（1）方法感悟：
如图①，在正方形ABCD中，点E，F分别为DC，BC边上的点，且满足∠EAF=45°，连接EF，求证DE+BF=EF．
感悟解题方法，并完成下列填空：
将△ADE绕点A顺时针旋转90°得到△ABG，此时AB与AD重合，由旋转可得：
AB=AD，BG=DE，∠1=∠2，∠ABG=∠D=90°，
∴∠ABG+∠ABF=90°+90°=180°，
因此，点G，B，F在同一条直线上．
∵∠EAF=45°∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°．
∵∠1=∠2，∴∠1+∠3=45°．
即∠GAF=∠
 
．
又AG=AE，AF=AF
∴△GAF≌
 
．
∴
 
=EF，故DE+BF=EF．
（2）方法迁移：
如图②，将Rt△ABC沿斜边翻折得到△ADC，点E，F分别为DC，BC边上的点，且∠EAF=
1
2
∠DAB．试猜想DE，BF，EF之间有何数量关系，并证明你的猜想．
（3）问题拓展：
如图③，在四边形ABCD中，AB=AD，E，F分别为DC，BC上的点，满足∠EAF=
1
2
∠DAB，试猜想当∠B与∠D满足什么关系时，可使得DE+BF=EF．请直接写出你的猜想（不必说明理由）．
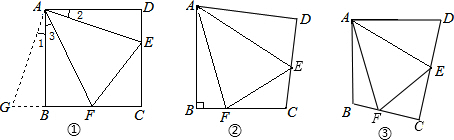
精英家教网
如图，将正方形纸片按图甲中的虚线对折得到图乙，再对折得到图丙，在图丙中沿虚线将△ABC（AB≠BC）剪下，再将△ABC展开铺平所得图形是（　　）
（1）如图，四边形ABCD是正方形，△ADF旋转一定角度后得到△ABE，如果AF=4，AB=7：
①写出图中的旋转过程；
②求BE的长；
③在图中作出延长BE与DF的交点G，并说明BG⊥DF．
（2）如图，将三角尺ABC（其中∠ABC=60°，∠C=90°）绕点B按顺时针转动一个角度到A1BC1的位置，使得点A、B、C1在同一条直线上，那么这个角度等于
A
A
．
A.120°    B.90°  C.60°     D.30°．
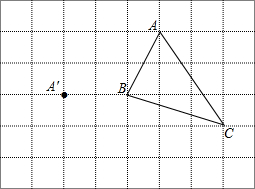精英家教网如图，将三角形ABC进行平移，使点A的对应点为点A′
（1）请你画出平移后所得的三角形A′B′C′（画图工具不限）．
（2）若每个小正方形的面积为1，求线段AC在平移中扫过的面积．
探究问题：
（1）方法感悟：
如图①，在正方形ABCD中，点E，F分别为DC，BC边上的点，且满足∠EAF=45°，连接EF，求证DE+BF=EF．
感悟解题方法，并完成下列填空：
将△ADE绕点A顺时针旋转90°得到△ABG，此时AB与AD重合，由旋转可得：
AB=AD，BG=DE，∠1=∠2，∠ABG=∠D=90°，
∴∠ABG+∠ABF=90°+90°=180°，
因此，点G，B，F在同一条直线上．
∵∠EAF=45°∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°．
∵∠1=∠2，∴∠1+∠3=45°．
即∠GAF=∠______．
又AG=AE，AF=AF
∴△GAF≌______．
∴______=EF，故DE+BF=EF．

（2）方法迁移：
如图②，将Rt△ABC沿斜边翻折得到△ADC，点E，F分别为DC，BC边上的点，且∠EAF=∠DAB．试猜想DE，BF，EF之间有何数量关系，并证明你的猜想．

（3）问题拓展：
如图③，在四边形ABCD中，AB=AD，E，F分别为DC，BC上的点，满足∠EAF=∠DAB，试猜想当∠B与∠D满足什么关系时，可使得DE+BF=EF．请直接写出你的猜想（不必说明理由）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网