Question

【题目】如图，AB是⊙O的直径，点C、D在⊙O上，AD与BC相交于点E．连接BD，作∠BDF＝∠BAD，DF与AB的延长线相交于点F．

（1）求证：DF是⊙O的切线；

（2）若DF∥BC，求证：AD平分∠BAC；

（3）在（2）的条件下，若AB＝10，BD＝6，求CE的长．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）．

【解析】

（1）如图，连结OD，只需推知OD⊥DF即可证得结论；

（2）根据平行线的性质得到∠FDB＝∠CBD，由圆周角的性质可得∠CAD＝∠BAD＝∠CBD＝∠BDF，即AD平分∠BAC；

（3）由勾股定理可求AD的长，通过△BDE∽△ADB，可得，可求DE＝，AE＝，由锐角三角函数可求CE的长．

（1）连接OD，CD，

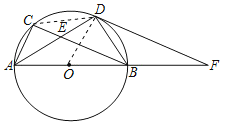
∵AB是直径，

∴∠ADB＝90°，

∴∠ADO+∠ODB＝90°，

∵OA＝OD，

∴∠BAD＝∠ADO，

∵∠BDF＝∠BAD，

∴∠BDF+∠ODB＝90°，

∴∠ODF＝90°，

∴OD⊥DF，

∴DF是⊙O的切线；

（2）∵DF∥BC，

∴∠FDB＝∠CBD，

∵，

∴∠CAD＝∠CBD，且∠BDF＝∠BAD，

∴∠CAD＝∠BAD＝∠CBD＝∠BDF，

∴AD平分∠BAC；

（3）∵AB＝10，BD＝6，

∴AD＝，

∵∠CBD＝∠BAD，∠ADB＝∠BDE＝90°，

∴△BDE∽△ADB，

∴，

∴，

∴DE＝，

∴AE＝AD﹣DE＝，

∵∠CAD＝∠BAD，

∴sin∠CAD＝sin∠BAD

∴

∴

∴CE＝