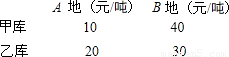题目内容
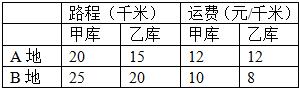
18、甲、乙两个仓库要向A、B两地运送水泥,已知甲库可调100吨水泥,乙库可调80吨水泥,A地需70吨水泥,B地需110吨水泥,甲、乙两个仓库到A、B两地的路程和运费如下表(表中运费栏“元/吨•千米”表示每吨水泥运送1千米所需人民币):
问:要使总运费最少,甲向A地运送

问:要使总运费最少,甲向A地运送
70
吨?分析:先设甲向A地运送水泥x吨,根据其中关系可以得到甲、乙两个仓库要向A、B两地分别运送水泥数,然后根据图表信息列出总运费和x的关系.
解答:解:又图表可知,甲库到A地的路费为20×12=240元,甲库到B地的路费为25×10=250元,乙库到A地的路费为15×12=180元,乙库到B地的路费为20×8=160元.
设甲向A地运送水泥x吨,则向B地运送100-x吨,乙向A地运送水泥70-x吨,向B地运送水泥110-(100-x)=10+x,x的取值范围为
则总运费为W=240x+250(100-x)+180(70-x)+160(10+x)=39200-30x,
有x的取值范围0≤x≤70,所以当x为70时,W=37100,W最小,
故答案为:70.
设甲向A地运送水泥x吨,则向B地运送100-x吨,乙向A地运送水泥70-x吨,向B地运送水泥110-(100-x)=10+x,x的取值范围为
则总运费为W=240x+250(100-x)+180(70-x)+160(10+x)=39200-30x,
有x的取值范围0≤x≤70,所以当x为70时,W=37100,W最小,
故答案为:70.
点评:本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.

练习册系列答案
相关题目
 27、甲,乙两个仓库要向A,B两地调运小麦,已知甲库可以调出80吨,乙库可以调出40吨.A地需要小麦50吨,B地需要70吨.甲,乙两库运往A,B两地的费用如下表:
27、甲,乙两个仓库要向A,B两地调运小麦,已知甲库可以调出80吨,乙库可以调出40吨.A地需要小麦50吨,B地需要70吨.甲,乙两库运往A,B两地的费用如下表: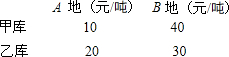 出40吨.A地需要小麦50吨,B地需要70吨.甲,乙两库运往A,B两地的费用如下表:
出40吨.A地需要小麦50吨,B地需要70吨.甲,乙两库运往A,B两地的费用如下表: