题目内容
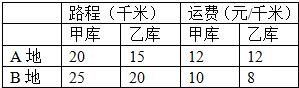
甲，乙两个仓库要向A，B两地调运小麦，已知甲库可以调出80吨，乙库可以调
出40吨．A地需要小麦50吨，B地需要70吨．甲，乙两库运往A，B两地的费用如下表：
（1）设甲库运往A地x吨，求总运费y（单位：元）与x之间的函数关系式；
（2）哪种方案总运费最省？哪种方案总运费最多？并求最省和最多的运费．
解：（1）已知甲库运往A地x吨，
则从甲库运往B地（80-x）吨，由乙库运往A地（50-x）吨，运往B地（x-10）吨．
所以y=10x+40（80-x）+20（50-x）+30（x-10）=3900-20x；
（2）根据已知可知10≤x≤50，
所以，当x=50时，总运费最省，为2900元；
当x=10时，总运费最多，为3700元．
分析：（1）根据总运费=甲库运往A地需要的费用+甲库运往B地需要的费用+乙库运往A地需要的费用+乙库运往B地需要的费用，经过化简得出y与x的关系式；
（2）根据函数的性质求出运费最省和最多的方案．
点评：一次函数的综合应用题常出现于销售、收费、行程等实际问题当中，利用一次函数求最值时，主要应用一次函数的性质．
则从甲库运往B地（80-x）吨，由乙库运往A地（50-x）吨，运往B地（x-10）吨．
所以y=10x+40（80-x）+20（50-x）+30（x-10）=3900-20x；
（2）根据已知可知10≤x≤50，
所以，当x=50时，总运费最省，为2900元；
当x=10时，总运费最多，为3700元．
分析：（1）根据总运费=甲库运往A地需要的费用+甲库运往B地需要的费用+乙库运往A地需要的费用+乙库运往B地需要的费用，经过化简得出y与x的关系式；
（2）根据函数的性质求出运费最省和最多的方案．
点评：一次函数的综合应用题常出现于销售、收费、行程等实际问题当中，利用一次函数求最值时，主要应用一次函数的性质．
练习册系列答案
相关题目
27、甲，乙两个仓库要向A，B两地调运小麦，已知甲库可以调出80吨，乙库可以调出40吨．A地需要小麦50吨，B地需要70吨．甲，乙两库运往A，B两地的费用如下表：
