Question

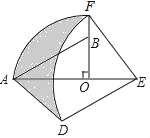
【题目】如图，分别以Rt△ABC的直角边AC，斜边AB为边向外作等边三角形△ACD和△ABE，F为AB的中点，连接DF，EF，∠ACB＝90°，∠ABC＝30°．则以下4个结论：①AC⊥DF；②四边形BCDF为平行四边形；③DA+DF＝BE；④其中，正确的 是（　　）

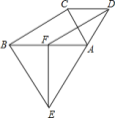
A.只有①②B.只有①②③C.只有③④D.①②③④

Answer 1

【答案】A

【解析】

根据平行四边形的判定定理判断②，根据平行四边形的性质和平行线的性质判断①，根据三角形三边关系判断③，根据等边三角形的性质分别求出△ACD、△ACB、△ABE的面积，计算即可判断④．

∵∠ACB=90°，∠ABC=30°，
∴∠BAC=60°，AC=AB，
∵△ACD是等边三角形，
∴∠ACD=60°，
∴∠ACD=∠BAC，
∴CD∥AB，
∵F为AB的中点，
∴BF=AB，
∴BF∥CD，CD=BF，
∴四边形BCDF为平行四边形，②正确；
∵四边形BCDF为平行四边形，
∴DF∥BC，又∠ACB=90°，
∴AC⊥DF，①正确；
∵DA=CA，DF=BC，AB=BE，BC+AC＞AB
∴DA+DF＞BE，③错误；
设AC=x，则AB=2x，
S△ACD= ，④错误，
故选：A．