题目内容
10、如图?ABCD中，过对角线BD上一点P作EF∥BC，GH∥AB，图中有（ ）对面积相等的平行四边形．分析：平行四边形的对角线将平行四边形分成两个面积相等的三角形．所以三角行ABD的面积等于三角形BCD的面积．三角形BGP的面积等于EBP的面积，三角形HPD的面积等于三角形PDF的面积，从而可得到AEPH的面积等于GCFP的面积，同时加上一个公共的平行四边形，可以得出答案有三个．
解答：解：∵ABCD为平行四边形，BD为对角线，
∴△ABD的面积等于△BCD的面积，
同理△BGP的面积等于△EBP的面积，△PFD的面积等于△HPD的面积，
∵△BCD的面积减去△BGP的面积和PDF的面积等于平行四边形PGCF的面积，△ABD的面积减去△EBP和△HPD的面积等于平行四边形AEPH的面积．
∴?PGCF的面积等于?AEPH的面积．
∴同时加上平行四边形PFDH和BGPE，
可以得出?AEFD面积和?HGCD面积相等，?ABGH和?BCFE面积相等．
所以有3对面积相等的平行四边形．
故选C．
∴△ABD的面积等于△BCD的面积，
同理△BGP的面积等于△EBP的面积，△PFD的面积等于△HPD的面积，
∵△BCD的面积减去△BGP的面积和PDF的面积等于平行四边形PGCF的面积，△ABD的面积减去△EBP和△HPD的面积等于平行四边形AEPH的面积．
∴?PGCF的面积等于?AEPH的面积．
∴同时加上平行四边形PFDH和BGPE，
可以得出?AEFD面积和?HGCD面积相等，?ABGH和?BCFE面积相等．
所以有3对面积相等的平行四边形．
故选C．
点评：本题考点平行四边形的性质．平行四边形的对角线将平行四边形分成两个面积相等的三角形．并且平行四边形的两条对角线交于一点，这个点是平行四边形的中心，也是两条对角线的中点，经过中心的任意一条直线可将平行四边形分成完全重合的两个图形．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
25、在图1-5中，正方形ABCD的边长为a，等腰直角三角形FAE的斜边AE=2b，且边AD和AE在同一直线上．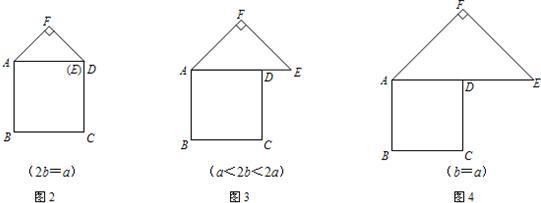
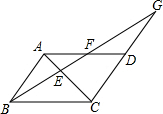如图，已知?ABCD中，过点B的直线与AC相交于点E、与AD相交于点F、与CD的延长线相交于点G，若BE=5，EF=2，则FG=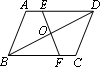
如图?ABCD中，过对角线BD上一点P作EF∥BC，GH∥AB，图中有___对面积相等的平行四边形．