题目内容
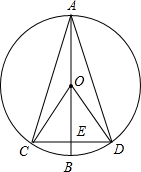
如图,直径AB垂直于弦CD,垂足为E,∠AOC=130°,则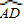 的度数为 °,
的度数为 °,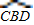 的度数为 °,∠CAD的度数为 °,∠ACD的度数为 °.
的度数为 °,∠CAD的度数为 °,∠ACD的度数为 °.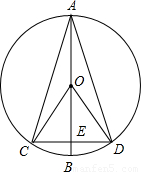
【答案】分析:由直径AB垂直于弦CD,根据垂径定理得EC=EB,得到AC=AD,所以∠AOD=∠AOC=130°,根据圆心角的度数等于它所对的弧的度数
得到弧AD的度数=130°;则有弧CBD=360°-2×130°=100°;再根据圆周角定理得到∠CAD= ×100°=50°;最后根据等腰三角形的性质和三角形的内角和定理即可求出∠ACD.
×100°=50°;最后根据等腰三角形的性质和三角形的内角和定理即可求出∠ACD.
解答:解:∵直径AB垂直于弦CD,
∴EC=EB,
∴AC=AD,
∴∠AOD=∠AOC=130°,
∴弧AD的度数=130°;
∴弧CBD=360°-2×130°=100°;
∴∠CAD= ×100°=50°;
×100°=50°;
∴∠ACD= (180°-50°)=65°.
(180°-50°)=65°.
故答案为:130,100,50,65.
点评:本题考查了在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等.也考查了圆心角的度数等于它所对的弧的度数以及圆周角定理.
得到弧AD的度数=130°;则有弧CBD=360°-2×130°=100°;再根据圆周角定理得到∠CAD=
 ×100°=50°;最后根据等腰三角形的性质和三角形的内角和定理即可求出∠ACD.
×100°=50°;最后根据等腰三角形的性质和三角形的内角和定理即可求出∠ACD.解答:解:∵直径AB垂直于弦CD,
∴EC=EB,
∴AC=AD,
∴∠AOD=∠AOC=130°,
∴弧AD的度数=130°;
∴弧CBD=360°-2×130°=100°;
∴∠CAD=
 ×100°=50°;
×100°=50°;∴∠ACD=
 (180°-50°)=65°.
(180°-50°)=65°.故答案为:130,100,50,65.
点评:本题考查了在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等.也考查了圆心角的度数等于它所对的弧的度数以及圆周角定理.

练习册系列答案
相关题目
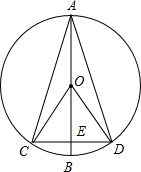 如图,直径AB垂直于弦CD,垂足为E,∠AOC=130°,则
如图,直径AB垂直于弦CD,垂足为E,∠AOC=130°,则

 如图,直径AB垂直于弦CD,垂足为E,∠AOC=130°,则
如图,直径AB垂直于弦CD,垂足为E,∠AOC=130°,则 的度数为________°,
的度数为________°, 的度数为________°,∠CAD的度数为________°,∠ACD的度数为________°.
的度数为________°,∠CAD的度数为________°,∠ACD的度数为________°. 如图,⊙O直径AB垂直于弦CD,垂足E是OB的中点,CD=6cm,则直径AB=________cm.
如图,⊙O直径AB垂直于弦CD,垂足E是OB的中点,CD=6cm,则直径AB=________cm.