题目内容
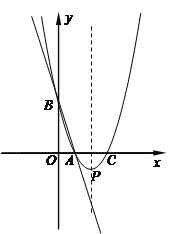
【题目】如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与x轴交于另一点C,其顶点为P.
(1)求a,k的值;
(2)抛物线的对称轴上是否存在一点M,使△ABM的周长最小,若存在,求出△ABM的周长;若不存在,请说明理由;
(3)若以AB为直径画圆,与抛物线的对称轴交于点N,求出点N坐标.
【答案】(1)a,k的值分别为1,﹣1;(2)![]() ,理由见解析;(3)点N的坐标为(2,2)或(2,1)
,理由见解析;(3)点N的坐标为(2,2)或(2,1)
【解析】(1)由条件可先求得A、B坐标,代入抛物线解析式可求得a、k的值;
(2)由A、C关于对称轴对称,连接BC交对称轴于点M,则M即为所求,由B、C可求得直线BC的解析式,可求得M点的坐标,容易求得其周长;
(3)可设N点坐标为(2,n),可分别表示出AB、AN、BN的长,由勾股定理可得到关于n的方程,可求得N点坐标.
(1)∵直线y=﹣3x+3与x轴、y轴分别交于点A、B,
∴A(1,0),B(0,3).
又∵抛物线抛物线y=a(x﹣2)2+k经过点A(1,0),B(0,3),
∴![]()
解得![]()
故a,k的值分别为1,﹣1;
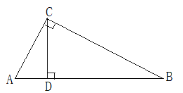
(2)如图1,存在这样的点M.连接BC与对称轴x=2的交点即为M点,这时△ABM的周长最小.
由抛物线对称性可得,点C坐标为(3,0),
△ABM的周长=AB+AM+BM
=AB+BC
=![]() ;
;
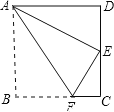
(3)如图2,由题意,可设N点的坐标为(2,n),对称轴x=2交x轴于点F,过点B作BE垂直于直线x=2于点E.
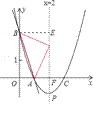
∵AB为所作圆的直径,N为所作圆与直线x=2的交点,
∴∠ANB=90°.
在Rt△ANF中,AN2=AF2+NF2=1+n2,
在Rt△BNE中,BN2=BE2+EN2=4+(3﹣n)2,
由勾股定理,得到方程1+n2+4+(3﹣n)2=12+32,
化简,得n2﹣3n +2=0,
解得 n1=2,n2=1,
∴点N的坐标为(2,2)或(2,1).

【题目】学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如表:
选手 | 表达能力 | 阅读理解 | 综合素质 | 汉字听写 |
甲 | 85 | 78 | 85 | 73 |
乙 | 73 | 80 | 82 | 83 |
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.