题目内容
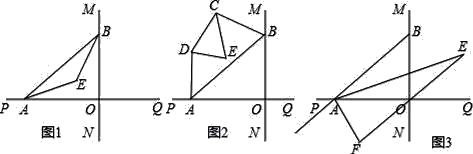
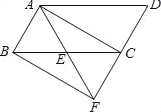
【题目】如图,四边形ABCD中,MA=MC,MB=MD,以AB为直径的O过点M且与DC延长线相切于点E.
(1)求证:四边形ABCD是菱形;
(2)若AB=4,求![]() 的长(结果请保留π)
的长(结果请保留π)
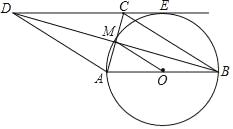
【答案】(1)见解析;(2)![]()
【解析】分析:(1)、首先根据MA=MC,MB=MD得出四边形为平行四边形,然后根据直径的性质得出∠AMB=90°,从而得出菱形;(2)、作CH⊥AB于点H,连接OE,根据菱形的性质得出∠BOM的度数,然后根据弧长的计算公式得出答案.
详解:(1)∵MA=MC,MB=MD, ∴四边形ABCD是平行四边形,
∵AB是⊙O的直径,且⊙O经过点M, ∴∠AMB=90°,即AC⊥BD,
∴四边形ABCD是菱形;
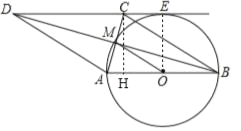
(2)如图,作CH⊥AB于点H,连接OE,
∵四边形ABCD是菱形,且AB=4, ∴DE∥AB,BC=AB=4,OA=OB=OE=2,
∵⊙O与DC相切于点E, ∴OE⊥DC, 则CH=OE=2,
在Rt△BCH中,由BC=2CH知∠CBH=30°, ∴∠OBM=![]() ∠CBH=15°, ∵OB=OM=2,
∠CBH=15°, ∵OB=OM=2,
∴∠BOM=150°, 则![]() 的长为
的长为![]() =
=![]() .
.

练习册系列答案
相关题目