Question

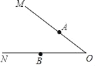
【题目】如图，已知∠MON，点A，B分别在OM，ON边上，且OA＝OB．

（1）求作：过点A，B分别作OM，ON的垂线，两条垂线的交点记作点D（保留作图痕迹，不写作法）；

（2）连接OD，若∠MON＝50°，则∠ODB＝　 　°．

Answer 1

【答案】(1)见解析;(2)65.

【解析】

（1）根据过直线上一点作直线垂线的方法作出垂线即可；

（2）利用全等三角形的判定与性质结合四边形内角和定理得出答案．

解：（1）如图，DA，DB即为所求垂线；

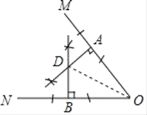
（2）连接OD，

∵DB⊥ON，DA⊥OM，

∴∠OBD＝∠OAD＝90°，∠MON＝50°，

∴∠ADB＝180°﹣50°＝130°．

在Rt△OBD与Rt△OAD中，

∵，

∴Rt△OBD≌Rt△OAD（HL），

∴∠ODB＝∠ADB＝65°．

故答案为：65．