题目内容
已知关于x的方程x2﹣2（k﹣1）x+k2=0有两个实数根x1，x2．
（1）求k的取值范围；
（2）若|x1+x2|=x1x2﹣1，求k的值．
（1）求k的取值范围；
（2）若|x1+x2|=x1x2﹣1，求k的值．
（1）
（2）k= -3
（2）k= -3解：（1）由已知得，方程有两个实数根
∴△=
∴
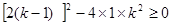
（2）∵x1+x2=2（k-1）, x1x2=k2, |x1+x2|=x1x2﹣1
∴
∵
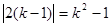
∴2k-2<0
∴2-2k=k2-1
解得k1="-3," k2=1(不合，舍去)
∴k= -3
∴△=
∴
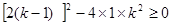
（2）∵x1+x2=2（k-1）, x1x2=k2, |x1+x2|=x1x2﹣1
∴
∵
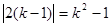
∴2k-2<0
∴2-2k=k2-1
解得k1="-3," k2=1(不合，舍去)
∴k= -3
练习册系列答案
相关题目
.
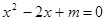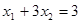，求m的值.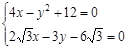
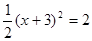的解为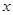 
，则可列方程 。
的解是（ ）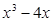
=