题目内容
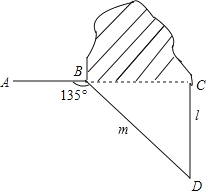
【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(结果保留根号)
【答案】直线L上距离D点400![]() 米的C处开挖.
米的C处开挖.
【解析】
首先证明△BCD是等腰直角三角形,再根据勾股定理可得CD2+BC2=BD2,然后再代入BD=800米进行计算即可.
∵CD⊥AC,
∴∠ACD=90°,
∵∠ABD=135°,
∴∠DBC=45°,
∴∠D=45°,
∴△BCD是等腰直角三角形,CB=CD,
在Rt△DCB中:CD2+BC2=BD2,
2CD2=8002,
CD=400![]() (米),
(米),
答:直线L上距离D点400![]() 米的C处开挖.
米的C处开挖.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目