题目内容
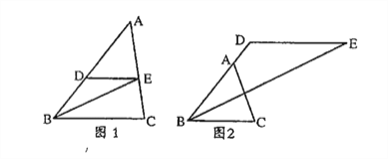
【题目】△ABC中,D是AB边上的一点,过点D作DE∥BC,∠ABC的角平分线于点E.
(1)如图1,当点E恰好在AC边上时,求证:∠ADE=2∠DEB;
(2)如图2,当点D在BA的延长线上时,其余条件不变,请直接写出∠ADE与∠DEB之间的数量关系,并说明理由。
【答案】(1)见解析 (2)∠ADE+2∠DEB=180°
【解析】试题分析:(1)根据角平分线的定义可得![]() ,再根据两直线平行,内错角相等可得
,再根据两直线平行,内错角相等可得![]() 再根据三角形的一个外角等于与它不相邻的两个内角的和证明即可;
再根据三角形的一个外角等于与它不相邻的两个内角的和证明即可;
(2)同理求出![]() 再根据三角形的内角和定理列式计算即可得解.
再根据三角形的内角和定理列式计算即可得解.
试题解析:证明:(1)∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵DE∥BC,
∴∠CBE=∠DEB,
在△BDE中,∠ADE=∠ABE+∠DEB=2∠DEB;
(2)同(1)可得∠DEB=∠CBE,
在△BDE中,![]()
所以,![]()

练习册系列答案
相关题目