题目内容
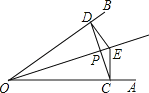
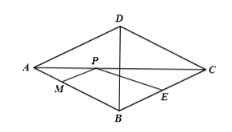
【题目】已知:如图,△ABC和△ADE是等腰直角三角形,∠BAC=∠DAE=90°,点C、D、E三点在同一直线上,连接BD.

(1)求证:△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.
【答案】(1)见解析;(2)BD=CE,BD⊥CE,理由见解析
【解析】
(1)由等腰直角三角形的性质可得AB=AC,AE=AD,∠BAC=∠EAD=90°,由“SAS”可证△BAD≌△CAE;
(2)由全等三角形的性质可得BD=CE,∠BDA=∠E=45°,所以∠BDE=∠BDA+∠ADE=90°,即可得到BD⊥CE.
解:(1)∵△ABC与△AED均为等腰直角三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=90°,
∴∠BAC+∠CAE=∠EAD+∠CAE,
即∠BAD=∠CAE,
在△BAD与△CAE中,
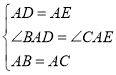 ,
,
∴△BAD≌△CAE(SAS),
(2)BD=CE,BD⊥CE.
∵△BAD≌△CAE,
∴BD=CE,∠BDA=∠E=45°,
∴∠BDE=∠BDA+∠ADE=90°,
∴BD⊥CE.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
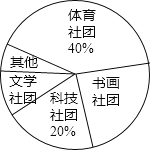
【题目】某校计划成立学生社团,要求每一位学生都选择一个社团,为了了解学生对不同社团的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查,规定每人必须并且只能在“文学社团”、“科学社团”、“书画社团”、“体育社团”和“其他”五项中选择一项,并将统计结果绘制了如下两个不完整的统计图表.
社团名称 | 人数 |
文学社团 | 18 |
科技社团 | a |
书画社团 | 45 |
体育社团 | 72 |
其他 | b |
请解答下列问题:
(1)a= ,b= ;
(2)在扇形统计图中,“书画社团”所对应的扇形圆心角度数为 ;
(3)若该校共有3000名学生,试估计该校学生中选择“文学社团”的人数.