题目内容
某县社会主义新农村建设办公室,为了解决该县甲,乙两村和一所中学长期存在的饮水困难问题,想在这三个地方的其中一处建一所供水站,由供水站直接铺设管道到另外两处.
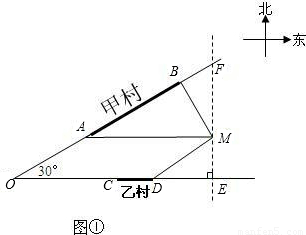
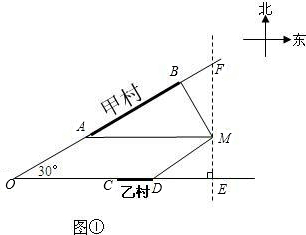
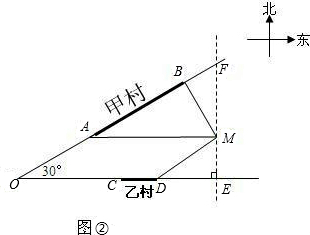
如图,甲,乙两村坐落在夹角为30°的两条公路的AB段和CD段(村子和公路的宽均不计),点M表示这所中学.点B在点M的北偏西30°的3km处,点A在点M的正西方向,点D在点M的南偏西60°的2
km处.
为使供水站铺设到另两处的管道长度之和最短,现有如下三种方案:
方案一:供水站建在点M处,请你求出铺设到甲村某处和乙村某处的管道长度之和的最小值;
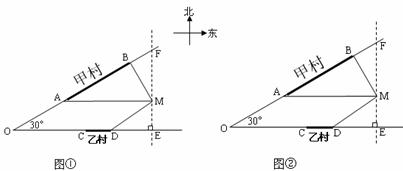
方案二:供水站建在乙村(线段CD某处),甲村要求管道铺设到A处,请你在图①中,画出铺设到点A和点M处的管道长度之和最小的线路图,并求其最小值;
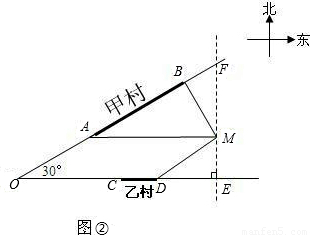
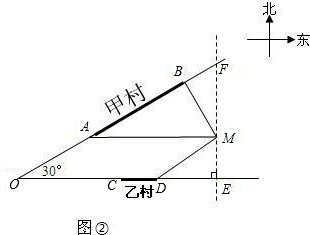
方案三:供水站建在甲村(线段AB某处),请你在图②中,画出铺设到乙村某处和点M处的管道长度之和最小的线路图,并求其最小值.
综上,你认为把供水站建在何处,所需铺设的管道最短?
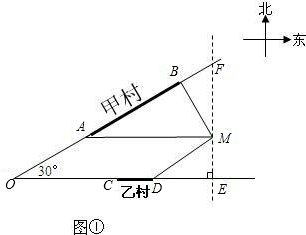
如图,甲,乙两村坐落在夹角为30°的两条公路的AB段和CD段(村子和公路的宽均不计),点M表示这所中学.点B在点M的北偏西30°的3km处,点A在点M的正西方向,点D在点M的南偏西60°的2
| 3 |
为使供水站铺设到另两处的管道长度之和最短,现有如下三种方案:
方案一:供水站建在点M处,请你求出铺设到甲村某处和乙村某处的管道长度之和的最小值;
方案二:供水站建在乙村(线段CD某处),甲村要求管道铺设到A处,请你在图①中,画出铺设到点A和点M处的管道长度之和最小的线路图,并求其最小值;
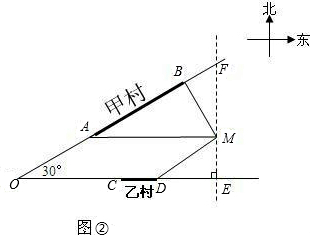
方案三:供水站建在甲村(线段AB某处),请你在图②中,画出铺设到乙村某处和点M处的管道长度之和最小的线路图,并求其最小值.
综上,你认为把供水站建在何处,所需铺设的管道最短?


方案一:
由题意可得:MB⊥OB,
∴点M到甲村的最短距离为MB,(1分)
∵点M到乙村的最短距离为MD,
∴将供水站建在点M处时,管道沿MD,MB线路铺设的长度之和最小,
即最小值为MB+MD=3+2
| 3 |
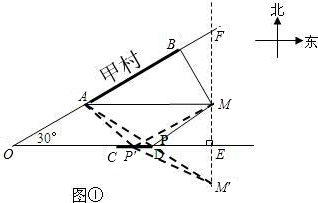
方案二:如图①,作点M关于射线OE的对称点M',则MM'=2ME,
连接AM'交OE于点P,PE∥AM,PE=
| 1 |
| 2 |
∵AM=2BM=6,∴PE=3,(4分)
在Rt△DME中,∵DE=DM?sin60°=2
| 3 |
| ||
| 2 |
ME=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴PE=DE,∴P点与D点重合,即AM'过D点,(6分)
在线段CD上任取一点P',连接P'A,P′M,P'M',
则P'M=P′M',
∵AP'+P'M'>AM',
∴把供水站建在乙村的D点处,管道沿DA,DM线路铺设的长度之和最小,
即最小值为AD+DM=AM'=
| AM2+MM′2 |
62+(2
|
| 3 |
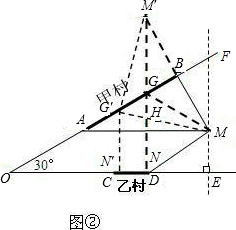
方案三:作点M关于射线OF的对称点M',作M'N⊥OE于N点,交OF于点G,交AM于点H,连接GM,则GM=GM',
∴M'N为点M'到OE的最短距离,即M'N=GM+GN
在Rt△M'HM中,∠MM'N=30°,MM'=6,
∴MH=3,∴NE=MH=3,
∵DE=3,∴N,D两点重合,即M'N过D点,
在Rt△M'DM中,DM=2
| 3 |
| 3 |
在线段AB上任取一点G',过G'作G'N'⊥OE于N'点,
连接G'M',G'M,
显然G'M+G'N'=G'M'+G'N'>M'D,
∴把供水站建在甲村的G处,管道沿GM,GD
线路铺设的长度之和最小,即最小值为GM+GD=M'D=4
| 3 |
综上,∵3+2
| 3 |
| 3 |
∴供水站建在M处,所需铺设的管道长度最短.(12分)

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 km处.
km处.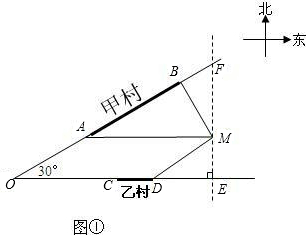
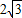 km处.
km处.