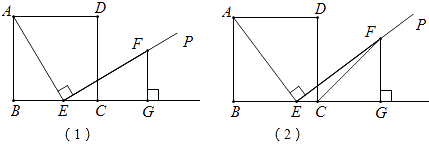题目内容
【题目】如图（1），E是正方形ABCD的边BC上的一个点（E与B、C两点不重合），过点E作射线EP⊥AE，在射线EP上截取线段EF，使得EF=AE；过点F作FG⊥BC交BC的延长线于点G．
（1）求证：FG=BE；
（2）连接CF，如图（2），求证：CF平分∠DCG；
（3）当 
= 
时，求sin∠CFE的值．
【答案】
（1）
证明：∵EP⊥AE，
∴∠AEB+∠GEF=90°，
又∵∠AEB+∠BAE=90°，
∴∠GEF=∠BAE，
又∵FG⊥BC，
∴∠ABE=∠EGF=90°，
在△ABE与△EGF中，
，
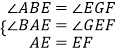∴△ABE≌△EGF（AAS），
∴FG=BE；
（2）
证明：由（1）知：BC=AB=EG，
∴BC﹣EC=EG﹣EC，
∴BE=CG，
又∵FG=BE，
∴FG=CG，
又∵∠CGF=90°，
∴∠FCG=45°= 
∠DCG，
∴CF平分∠DCG
（3）
解：如图，作CH⊥EF于H，
∵∠HEC=∠GEF，∠CHE=∠FGE=90°，
∴△EHC∽△EGF，
∴ 
= 
，
根据 
= 
，设BE=3a，则EC=a，EG=4a，FG=CG=3a，
∴EF=5a，CF=3 
a，
∴ 
= 
，HC= 
a，
∴sin∠CFE= 
= 
．
【解析】（1）根据同角的余角相等得到一对角相等，再由一对直角相等，且AE=EF，利用AAS得到三角形ABE与三角形EFG全等，利用全等三角形的对应边相等即可得证；（2）由（1）得到BC=AB=EG，利用等式的性质得到BE=CG，根据FG=BE，等量代价得到FG=CG，即三角形FCG为等腰直角三角形，得到∠FCG=45°，即可得证；（3）如图，作CH⊥EF于H，则△EHC∽△EGF，利用相似得比例，根据BE与BC的比值，设出BE，EC，以及EG，FG，利用勾股定理表示出EF，CF，进而表示出HC，在直角三角形HC中，利用锐角三角函数定义即可求出sin∠CFE的值．
