题目内容
【题目】已知:在四边形 ABCD 中,∠A+∠C=180°,DB 平分∠ADC.
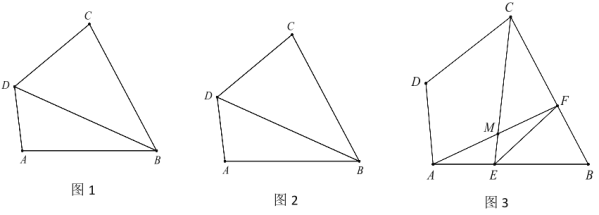
(1)如图 1求证:AB=BC
(2)如图 2,若∠ADB=60°,,试判断△ABC 的形状,并说明理由.
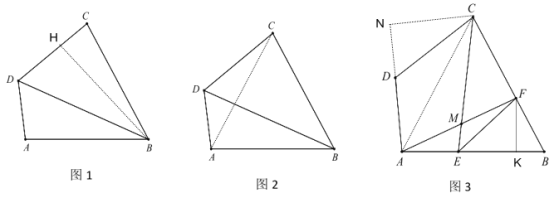
(3)如图 3,在(2)得条件下,在 AB 上取一点 E, BC 上取一点 F,连接 CE、AF 交于点 M,连接 EF,若∠CMF=60°,AD=EF=7,CD=8(CF﹥BF),求 AE 的长.
【答案】(1)见解析;(2)△ABC是等边三角形,理由见解析;(3)AE=5.
【解析】
(1)在DC上取一点H使DH=DA,易证△DAB≌△DHB,可得AB=HB,∠A=∠DHB,然后根据等角的补角相等以及等角对等边可得HB=BC,易证结论;
(2)连结AC,根据角平分线的定义和四边形内角和定理求出∠ABC =60°,即可得到△ABC是等边三角形;
(3)过点C作CN⊥AD交AD的延长线于点N,根据含30°直角三角形的性质求出DN=4,NC=![]() ,然后利用勾股定理求得AB= AC=13,由ASA证明△CAE≌△ABF,得到AE=BF,过点F作FK⊥AB,设BK=x,然后用含x的式子表示出FK和EK,在Rt△EFK中通过勾股定理列方程,求出x的值即可得解(注意舍去不合题意的解).
,然后利用勾股定理求得AB= AC=13,由ASA证明△CAE≌△ABF,得到AE=BF,过点F作FK⊥AB,设BK=x,然后用含x的式子表示出FK和EK,在Rt△EFK中通过勾股定理列方程,求出x的值即可得解(注意舍去不合题意的解).
解:(1)如图1,在DC上取一点H使DH=DA,
在△DAB和△DHB中,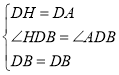 ,
,
∴△DAB≌△DHB(SAS),
∴AB=HB,∠A=∠DHB,
∵∠A+∠C=180°,∠DHB+∠BHC=180°,
∴∠C=∠BHC,
∴HB=BC,
∴AB=BC;
(2)△ABC是等边三角形,
理由:如图2,连结AC,
∵∠ADB=60°,∠A+∠C=180°,
∴∠ADC=120°,
∴∠ABC=180°-∠ADC=60°,
又由(1)得AB=BC,
∴△ABC是等边三角形;
(3)过点C作CN⊥AD交AD的延长线于点N,
∵∠ADC=120°,CD=8,
∴∠NDC=60°,
∴DN=4,NC=![]() ,
,
∴AN=AD+DN=11,
∴AC=![]() ,
,
∴AB= AC=13,
∵∠ACE=∠CMF-∠CAM=60°-∠CAM,∠FAB=60°-∠CAM,
∴∠ACE=∠FAB,
在△CAE和△ABF中,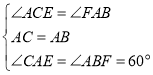 ,
,
∴△CAE≌△ABF(ASA),
∴AE=BF,
过点F作FK⊥AB,
设BK=x,则BF=2x,FK=![]() x,
x,
∴AE=BF=2x,
∴EK=AB-AE-BK=13-3x,
在Rt△EFK中,EF2=EK2+FK2,
∴72=(13-3x)2+(![]() x)2,
x)2,
解得:x1=![]() ,x2=4(舍去),
,x2=4(舍去),
∴AE=2x=5.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案