题目内容
如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=50º,求∠BAC的度数。
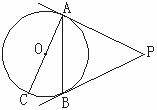

25°
分析:连接OB,根据切线的性质定理以及四边形的内角和定理得到∠AOB=180°-∠P=130°,再根据等边对等角以及三角形的内角和定理求得∠BAC的度数。
解答:
解:连接OB,
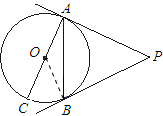
∵PA、PB是⊙O的切线,A、B为切点,
∴∠PAO=∠PBO=90°,
∴∠AOB=180°-∠P=130°,
∵OA=OB,
∴∠BAC=25°。

练习册系列答案
相关题目
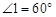 ,
,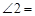 ▲
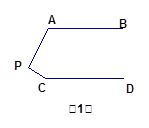
▲ 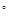 时,AB∥CD.
时,AB∥CD.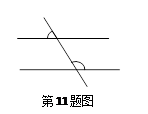
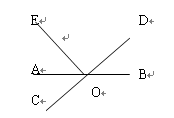
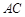 、
、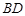 相交于点
相交于点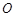 ,若
,若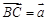 ,
,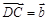 ,则( )
,则( )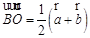 ;
;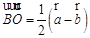 ;
;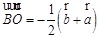 ;
; .
.