题目内容
【题目】已知正方形![]() 的边长为4,
的边长为4,![]() 、
、![]() 分别为直线
分别为直线![]() 、
、![]() 上两点.
上两点.
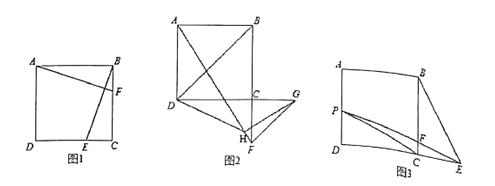
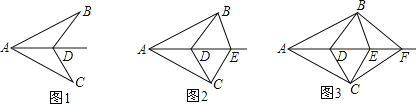
(1)如图1,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() ,求证:
,求证:![]() .
.
(2)如图2,点![]() 为
为![]() 延长线上一点,作
延长线上一点,作![]() 交
交![]() 的延长线于
的延长线于![]() ,作
,作![]() 于
于![]() ,求
,求![]() 的长.
的长.
(3)如图3,点![]() 在
在![]() 的延长线上,
的延长线上,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,直线
,直线![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,直接写出
,直接写出![]() 与
与![]() 的函数关系式.
的函数关系式.
【答案】(1)详见解析;(2)4;(3)![]()
【解析】
(1)先证出![]() ,得到
,得到![]() ,则有
,则有![]() ;
;
(2)延长![]() 交
交![]() 的延长线于
的延长线于![]() ,先证出
,先证出![]() ,得到
,得到![]() ,再由直角三角形的性质得到
,再由直角三角形的性质得到![]() ;
;
(3)过![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,先证得
,先证得![]() 得到
得到![]() ,再进一步得到
,再进一步得到![]() 及
及![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() .
.
(1)证明:∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)解:延长![]() 交
交![]() 的延长线于
的延长线于![]() ,
,
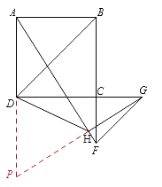
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
(3)![]() .
.
证明:过![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,
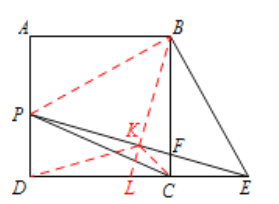
则![]() ,易得
,易得![]()
∴![]() ,
,
∴![]() ,
,
由此可证![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
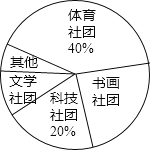
【题目】某校计划成立学生社团,要求每一位学生都选择一个社团,为了了解学生对不同社团的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查,规定每人必须并且只能在“文学社团”、“科学社团”、“书画社团”、“体育社团”和“其他”五项中选择一项,并将统计结果绘制了如下两个不完整的统计图表.
社团名称 | 人数 |
文学社团 | 18 |
科技社团 | a |
书画社团 | 45 |
体育社团 | 72 |
其他 | b |
请解答下列问题:
(1)a= ,b= ;
(2)在扇形统计图中,“书画社团”所对应的扇形圆心角度数为 ;
(3)若该校共有3000名学生,试估计该校学生中选择“文学社团”的人数.