题目内容
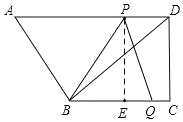
【题目】如图,在四边形ABCD中,AD∥BC,∠ADC=90°,BC=8,DC=6,AD=10,动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动,设运动的时间为t(秒)。

(1)当点P运动t秒后,AP=____________(用含t的代数式表示);
(2)若四边形ABQP为平行四边形,求运动时间t;
(3)当t为何值时,△BPQ是以BQ或BP为底边的等腰三角形;
【答案】(1)10-2t;(2)t=2(3)t=![]() 或t=
或t=![]() .
.
【解析】
(1)根据AP=AD-DP即可写出;
(2)当四边形ABQP为平行四边形时,AP=BQ,即可列方程进行求解;
(3)分两种情况讨论:①若PQ=BQ,在Rt△PQE中,由PQ2=PE2+EQ2,PQ=BQ,将各数据代入即可求解;②若PB=PQ,则BQ=2EQ,列方程即可求解.
(1)∵动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,
∴AP=AD-DP=10-2t,
故填:10-2t;
(2)∵四边形ABQP为平行四边形时,∴AP=BQ,
∵BQ=BC-CQ=8-t,
∴10-2t=8-t,解得t=2,
(3)如图,过点P作PE⊥BC于E,
①当∠BQP为顶角时,PQ=BQ,BQ=8-t,PE=CD=6,EQ=CE-CQ=2t-t=t,
在Rt△PQM中,由PQ2=PE2+EQ2,又PQ=BQ,
∴(8-t)2=62+t2,
解得t=![]()
②当∠BPQ为顶角时,则BP=PQ
由BQ=2EQ,即8-t=2t
解得t=![]()
故 t=![]() 或t=
或t=![]() 时,符合题意.
时,符合题意.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目