题目内容
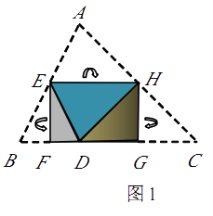
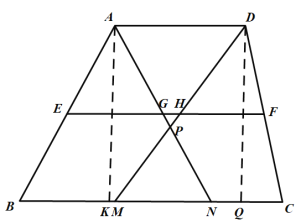
【题目】梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 在
在![]() 上,
上,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() 和
和![]() 分别与
分别与![]() 交于
交于![]() 和
和![]() ,
,![]() 和
和![]() 交于点
交于点![]() .
.
(1)求证:![]() ;
;
(2)当点![]() 在四边形
在四边形![]() 内部时,设
内部时,设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)当![]() 时,求
时,求![]() 的长.
的长.

【答案】(1)证明见解析;(2)![]()
![]() ;(3)3或
;(3)3或![]() .
.
【解析】
(1)由中位线的性质,角平分线的定义和平行线的性质得出![]() ,易证
,易证![]() ,则结论可证;
,则结论可证;
(2)过![]() 作
作![]() 交
交![]() 于点K,过点D作
于点K,过点D作![]() 交
交![]() 于点
于点![]() ,则得到矩形
,则得到矩形![]() ,则有
,则有![]() ,
,![]() ,然后利用(1)中的结论有
,然后利用(1)中的结论有![]() ,
, ![]() ,在
,在![]() 中,利用含30°的直角三角形的性质可得出QC,DQ的长度,然后在
中,利用含30°的直角三角形的性质可得出QC,DQ的长度,然后在![]() 中利用勾股定理即可找到y关于x的函数关系式;
中利用勾股定理即可找到y关于x的函数关系式;
(3)分两种情况:点![]() 在梯形
在梯形![]() 内部和点
内部和点![]() 在梯形
在梯形![]() 内部,当点
内部,当点![]() 在梯形
在梯形![]() 内部时,有
内部时,有![]() ;当点
;当点![]() 在梯形
在梯形![]() 内部时,有
内部时,有![]() ,分别结论(2)中的关系式即可求出EG的长度.
,分别结论(2)中的关系式即可求出EG的长度.
(1)证明:![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,
![]() .
.
![]() 平分
平分![]() ,
,
![]() .
.
又![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 点
点![]() 是
是![]() 的中点,
的中点,
![]() .
.
![]() .
.
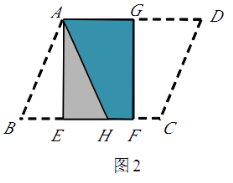
(2)过![]() 作
作![]() 交
交![]() 于点K,过点D作
于点K,过点D作![]() 交
交![]() 于点
于点![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴四边形![]() 是矩形,
是矩形,
![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
同理:![]() .
.
在![]() 中,
中,
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
在![]() 中,
中,![]() .
.
![]() ,
,
即![]() .
.
![]()
![]() .
.
(3)①点![]() 在梯形
在梯形![]() 内部.
内部.
∵![]() 是梯形
是梯形![]() 的中位线,
的中位线,
![]() ,
,
即![]() .
.
解得:![]() ,
,
即![]() .
.
②点![]() 在梯形
在梯形![]() 内部.
内部.
同理:![]() .
.
解得:![]() ,
,
即![]() .
.
综上所述,EG的长度为3或![]() .
.

练习册系列答案
相关题目
【题目】某商场用2700元购进甲、乙两种商品共100件,这两种商品的进价、标价如下表所示:
| 甲种 | 乙种 |
进价(元/件) | 15 | 35 |
标价(元/件) | 20 | 45 |
(1)求购进两种商品各多少件?
(2)商品将两种商品全部卖出后,获得的利润是多少元?