题目内容
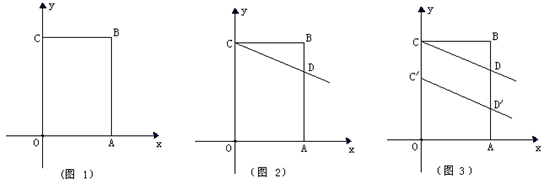
如图,长方形OABC中,O为平面直角坐标系的原点,A、C两点的坐标分别为(3,0),(0,5),点B在第一象限内.
(1)如图1,写出点B的坐标( );
(2)如图2,若过点C的直线CD交线段AB于点D,且把长方形OABC的周长分为3:1两部分,求点D的坐标;
(3)如图3,将(2)中的线段CD向下平移2个单位,得到C/D/,试计算四边形OAD/C/的面积.
(1)如图1,写出点B的坐标( );
(2)如图2,若过点C的直线CD交线段AB于点D,且把长方形OABC的周长分为3:1两部分,求点D的坐标;
(3)如图3,将(2)中的线段CD向下平移2个单位,得到C/D/,试计算四边形OAD/C/的面积.

(1)点B(3,5);(2)(3,4);(3)7.5.
试题分析:(1)点B的横坐标等于点A的横坐标,点B的纵坐标等于点C的纵坐标,从而求得点B的坐标;
(2)分两种情况讨论,并把不合题意的舍去即可;
(3)根据平移的性质,得C′(0,3),D′(3,2),然后再求四边形OAD′C′的面积.
(1)点B(3,5)
(2)过C作直线CD交AB于D,

由图可知:OC=AB=5,OA=CB=3.
①当(CO+OA+AD):(DB+CB)=1:3时
即:(5+3+AD):(5-AD+3)=1:3
8-AD=3(8+AD)
AD=-4(不合题意,舍去)
②当(DB+CB):(CO+OA+AD)=1:3时
即:(5-AD+3):(5+3+AD)=1:3
8+AD=3(8-AD)
AD=4
∴点D的坐标为(3,4)
(3)由题意知:C′(0,3),D′(3,2)
由图可知:OA=3,AD′=2,OC′=3
∴S四边形OAD′C″=
 (OC′+AD′)•OA=
(OC′+AD′)•OA= ×(3+2)×3=7.5.
×(3+2)×3=7.5.
练习册系列答案
相关题目
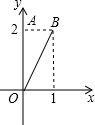
 ,0),(0,3),(3,3),(4,0).
,0),(0,3),(3,3),(4,0).