题目内容
 已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF(如图所示).
已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF(如图所示).
(1)添加条件∠A=∠D,∠OEF=∠OFE,求证:AB=DC.
(2)分别将“∠A=∠D”记为①,“∠OEF=∠OFE”记为②,“AB=DC”记为③,
若添加条件②、③,以①为结论构成另一个命题,则该命题是________命题
(选择“真”或“假”填入空格,不必证明).
(1)证明: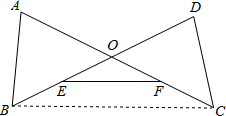 连接BC,
连接BC,
∵E为OB的中点,F为OC的中点,
∴EF∥BC,
∴∠OEF=∠OBC,∠OFE=∠OCB,
∵∠OEF=∠OFE,
∴∠OBC=∠OCB,
即∠ACB=∠DBC,
在△ABC和△DCB中
∵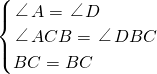 ,
,
∴△ABC≌△DCB(AAS),
∴AB=DC.
(2)解:以②③为条件,①为结论的命题是假命题,
理由是:根据AB=DC,BC=BC和∠ACB=∠DBC不能推出△ABC和△DCB全等,
故答案为:假.
分析:(1)连接BC,根据三角形中位线得出EF∥BC,推出∠OEF=∠OBC,∠OFE=∠OCB,推出∠OBC=∠OCB,根据AAS证△ABC≌△DCB即可;
(2)全等三角形的判定定理有SAS,AAS,ASA,SSS,看看根据已知能否推出符合的三个条件即可.
点评:本题考查了全等三角形的性质和判定,三角形的中位线,平行线的性质,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,三角形的中位线平行于第三边,并且等于第三边的一半.
 连接BC,
连接BC,∵E为OB的中点,F为OC的中点,
∴EF∥BC,
∴∠OEF=∠OBC,∠OFE=∠OCB,
∵∠OEF=∠OFE,
∴∠OBC=∠OCB,
即∠ACB=∠DBC,
在△ABC和△DCB中
∵
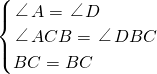 ,
,∴△ABC≌△DCB(AAS),
∴AB=DC.
(2)解:以②③为条件,①为结论的命题是假命题,
理由是:根据AB=DC,BC=BC和∠ACB=∠DBC不能推出△ABC和△DCB全等,
故答案为:假.
分析:(1)连接BC,根据三角形中位线得出EF∥BC,推出∠OEF=∠OBC,∠OFE=∠OCB,推出∠OBC=∠OCB,根据AAS证△ABC≌△DCB即可;
(2)全等三角形的判定定理有SAS,AAS,ASA,SSS,看看根据已知能否推出符合的三个条件即可.
点评:本题考查了全等三角形的性质和判定,三角形的中位线,平行线的性质,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
相关题目
 14、已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF.(1)添加条件∠A=∠D,OE=OF,试说明:AB=DC;
14、已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF.(1)添加条件∠A=∠D,OE=OF,试说明:AB=DC;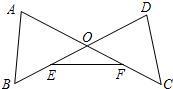 26、已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF(如图所示).
26、已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF(如图所示). 16、如图,已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF.若∠A=∠D,∠OEF=∠OFE,求证:AB=DC.
16、如图,已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF.若∠A=∠D,∠OEF=∠OFE,求证:AB=DC. 已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF(如图所示).
已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF(如图所示).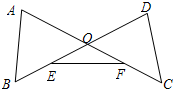 已知线段AC与BD相交于点O,联结AB、DC,E为OB的中点,F为OC的中点,连接EF.
已知线段AC与BD相交于点O,联结AB、DC,E为OB的中点,F为OC的中点,连接EF.