题目内容
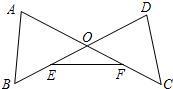 26、已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF(如图所示).
26、已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF(如图所示).(1)添加条件∠A=∠D,∠OEF=∠OFE,求证:AB=DC.
(2)分别将“∠A=∠D”记为①,“∠OEF=∠OFE”记为②,“AB=DC”记为③,添加条件①、③,以②为结论构成命题1,添加条件②、③,以①为结论构成命题2.命题1是命题,命题2是命题(选择“真”或“假”填入空格).
分析:(1)要证AB=DC,可考虑证△AOB≌△DOC.
(2)根据已知及全等三角形的判定方法对两个命题进行分析,从而判断其真假.
(2)根据已知及全等三角形的判定方法对两个命题进行分析,从而判断其真假.
解答:证明:(1)∵E为OB的中点,F为OC的中点,
∴OB=2OE,OC=2OF.
∵∠OEF=∠OFE,
∴OE=OF.
∴OB=OC.
在△AOB与△DOC中,
∠A=∠D,∠AOB=∠DOC,OB=OC,
∴△AOB≌△DOC(AAS).
∴AB=DC.
(2)对于命题1,可证△AOB≌△DOC得到OB=OC,再得OE=OF,从而能得到∠OEF=∠OFE,故其是真命题;
对于命题2,由所给的条件不能证明△AOB≌△DOC,因此其是假命题.
∴OB=2OE,OC=2OF.
∵∠OEF=∠OFE,
∴OE=OF.
∴OB=OC.
在△AOB与△DOC中,
∠A=∠D,∠AOB=∠DOC,OB=OC,
∴△AOB≌△DOC(AAS).
∴AB=DC.
(2)对于命题1,可证△AOB≌△DOC得到OB=OC,再得OE=OF,从而能得到∠OEF=∠OFE,故其是真命题;
对于命题2,由所给的条件不能证明△AOB≌△DOC,因此其是假命题.
点评:本题考查的是全等三角形的判定,要牢记全等三角形的判定条件,要记住SSA和AAA是不能证得两三角形全等的.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 14、已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF.(1)添加条件∠A=∠D,OE=OF,试说明:AB=DC;
14、已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF.(1)添加条件∠A=∠D,OE=OF,试说明:AB=DC; 16、如图,已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF.若∠A=∠D,∠OEF=∠OFE,求证:AB=DC.
16、如图,已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF.若∠A=∠D,∠OEF=∠OFE,求证:AB=DC. 已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF(如图所示).
已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF(如图所示).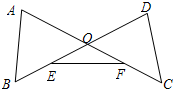 已知线段AC与BD相交于点O,联结AB、DC,E为OB的中点,F为OC的中点,连接EF.
已知线段AC与BD相交于点O,联结AB、DC,E为OB的中点,F为OC的中点,连接EF.