题目内容
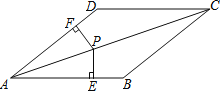
【题目】在四边形ABCD中,AB//CD,∠B=∠D.
(1)求证:四边形ABCD为平行四边形;
(2)若点P为对角线AC上的一点,PE⊥AB于E,PF⊥AD于F,且PE=PF,求证:四边形ABCD是菱形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据平行线的性质和平行四边形的判定证明即可;
(2)根据角平分线的性质和菱形的判定证明即可.
试题解析:(1)∵AB∥CD,
∴∠DCA=∠BAC,
在△ADC与△ABC中,
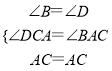 ,
,
∴△ADC≌△ABC(AAS),
∴AB=DC,
∵AB∥CD,
∴四边形ABCD为平行四边形;
(2)∵四边形ABCD为平行四边形,
∴∠DAB=∠DCB,
∵PE⊥AB于E,PF⊥AD于F,且PE=PF,
∴∠DAC=∠BAC=∠DCA=∠BCA,
∴AB=BC,
∴四边形ABCD是菱形.

练习册系列答案
相关题目