题目内容
设a,b是一个直角三角形两条直角边的长,且(a2+b2)(a2+b2+1)=12,则这个直角三角形的斜边长为________.

分析:根据勾股定理c2=a2+b2代入方程求解即可.
解答:∵a,b是一个直角三角形两条直角边的长
设斜边为c,
∴(a2+b2)(a2+b2+1)=12,根据勾股定理得:c2(c2+1)-12=0
即(c2-3)(c2+4)=0,
∵c2+4≠0,
∴c2-3=0,
解得c=
 或c=-
或c=- (舍去).
(舍去).则直角三角形的斜边长为
 .
.故答案为:

点评:本题考查的是利用勾股定理求直角三角形的斜边,需同学们灵活掌握.

练习册系列答案
相关题目
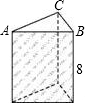 如图,是一个直三棱柱的模型,其底面是两直角边长分别为3cm、4cm的直角三角形,侧棱长都是8cm.
如图,是一个直三棱柱的模型,其底面是两直角边长分别为3cm、4cm的直角三角形,侧棱长都是8cm.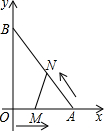 (2012•湛江)如图,在平面直角坐标系中,直角三角形AOB的顶点A、B分别落在坐标轴上.O为原点,点A的坐标为(6,0),点B的坐标为(0,8).动点M从点O出发.沿OA向终点A以每秒1个单位的速度运动,同时动点N从点A出发,沿AB向终点B以每秒
(2012•湛江)如图,在平面直角坐标系中,直角三角形AOB的顶点A、B分别落在坐标轴上.O为原点,点A的坐标为(6,0),点B的坐标为(0,8).动点M从点O出发.沿OA向终点A以每秒1个单位的速度运动,同时动点N从点A出发,沿AB向终点B以每秒 个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).
个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).
 个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).
个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).
 如图,是一个直三棱柱的模型,其底面是两直角边长分别为3cm、4cm的直角三角形,侧棱长都是8cm.
如图,是一个直三棱柱的模型,其底面是两直角边长分别为3cm、4cm的直角三角形,侧棱长都是8cm.