题目内容
【题目】为了美化环境,学校准备在如图所示的矩形ABCD空地上进行绿化,规划在中间的一块四边形MNPQ上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ,已知BC=30米,AB=42米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.
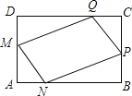
(1)分别求y1和y2与x之间的函数关系式(不要求写出自变量的取值范围);
(2)当AN的长为多少米时,种花的面积为640平方米?
(3)若种花每平方米需200元,铺设草坪每平方米需100元,现设计要求种花的面积不大于640平方米,设学校所需费用W(元),求W与x之间的函数关系式,并求出学校所需费用的最大值.
【答案】(1)y1=-2x2+72x;![]() ;(2)当AN的长为16米或20米时种花的面积为640平方米;(3)W=-200(x-18)2+190800,190000.
;(2)当AN的长为16米或20米时种花的面积为640平方米;(3)W=-200(x-18)2+190800,190000.
【解析】
(1)根据三角形面积公式可得y2的解析式,再用长方形面积减去y2,即可得y1的函数解析式;
(2)根据题意把y1=640代入y1=-2x2+72x得关于x的方程,解方程即可得;
(3)列出总费用的函数解析式,将其配方成顶点式,根据花的面积不大于640平方米可得x的范围,结合此范围根据二次函数的性质即可得函数的最大值,从而得解.
解:(1)根据题意,得![]()
![]() ,y1=42×30-y2=-2x2+72x;
,y1=42×30-y2=-2x2+72x;
(2)根据题意,把y1=640代入y1=-2x2+72x得:-2x2+72x=640,
解得:x1=16,x2=20,
故当AN的长为16米或20米时种花的面积为640平方米;
(3)设总费用为W元,
则W=200(-2x2+72x)+100(2x2-72x+1260)=-200(x-18)2+190800,
由(2)知当0<x≤16或20≤x≤30时,y1≤640,
在W=-200(x-18)2+190800中,当x<18时,W随x的增大而增大,当x>18时,W随x的增大而减小,
∴当x=16时,W取得最大值,最大值W=190000,
当x=20时,W取得最大值,最大值W=190000,
∴学校所需费用的最大值为190000元.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案【题目】《国家学生体质健康标准》规定:体质测试成绩达到90.0分及以上的为优秀;达到80.0分至89.9分的为良好;达到60.0分至79.9分的为及格;59.9分及以下为不及格,某校为了了解九年级学生体质健康状况,从该校九年级学生中随机抽取了10%的学生进行体质测试,测试结果如下面的统计表和扇形统计图所示。
各等级学生平均分统计表
等级 | 优秀 | 良好 | 及格 | 不及格 |
平均分 | 92.1 | 85.0 | 69.2 | 41.3 |
各等级学生人数分布扇形统计图

(1)扇形统计图中“不及格”所占的百分比是 ;
(2)计算所抽取的学生的测试成绩的平均分;
(3)若所抽取的学生中所有不及格等级学生的总分恰好等于某一个良好等级学生的分数,请估计该九年级学生中约有多少人达到优秀等级。