题目内容
【题目】如图,在数轴上每相邻两点之间的距离为一个单位长度.![]()
(1)若点A,B,C,D对应的数分别是a,b,c,d, 则可用含![]() 的整式表示d为__________,
的整式表示d为__________,
若3d-2a=14,则b=____________ c=_____________(填具体数值)
(2)在(1)的条件下, 点A以4个单位/秒的速度沿着数轴的正方向运动,同时点B以2个单位/秒的速度沿着数轴的正方向运动,当点A到达D点处立刻返回,与点B在数轴的
某点处相遇,求相遇点所对应的数.
(3)如果点A以2个单位/秒的速度沿着数轴的负方向运动,同时点B以4个单位/秒的
速度沿着数轴的正方向运动,是否存在某时刻使得点A与点B 到点C的距离相等,若存在请求出时间t,若不存在请说明理由.
【答案】 (1)a+8 -12 -7;(2)-6;(3)见解析
【解析】试题分析:(1)根据数轴可知d=a+8,然后代入等式求出a的值,再根据数轴确定出b、c即可;
(2)根据相遇问题求得相遇时间,再计算即可求解;
(3)根据AB=AC列出方程,再分两种情况讨论即可求解.
试题解析:解: (1)d=a+8,∵3(a+8)-2a=14,∴a=-10,b=a-2=-12,c=a+3=-7;
(2) ∵AD=-2-(-10)=-2+10=8,BD=-2-(-12)=-2+12=10, ∴两点的路程之和为:8+10=18.
∴两点的相遇时间为: 18÷(4+2)=3,∴相遇点所表示的数为:-12+3×2=-6;
(3) 存在![]() 或4时,点A与点B到点C的距离相等.理由如下:
或4时,点A与点B到点C的距离相等.理由如下:
①当点A与点B相遇时: ![]() ,
,
②当点A在点C右侧时:
t秒时点A、B表示的数分别为: -10-2t;-12+4t
此时点A到点C的距离为:-7-(-10-2t)=2t+3,
点B到点C的距离为:-12+4t-(-7)=4t-5,
∴2t+3=4t-5,
解得t=4,
综上所述:当![]() 或4时,点A与点B到点C的距离相等.
或4时,点A与点B到点C的距离相等.

 名校课堂系列答案
名校课堂系列答案【题目】6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成统计图. 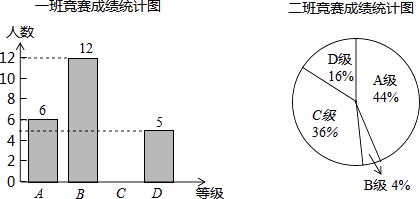
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | d | 80 | c |
(1)把一班竞赛成绩统计图补充完整;
(2)写出表中a、b、c的值:
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | d | 80 | c |
(3)请从平均数和中位数方面比较一班和二班的成绩,对这次竞赛成绩的结果进行分析.
【题目】为了让同学们了解自己的体育水平,初二1班的体育康老师对全班45名学生进行了一次体育模拟测试(得分均为整数)成绩满分为10分,成绩达到9分以上(包含9分)为优秀,成绩达到6分以上(包含6分)为合格,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下: 
初二1班体育模拟测试成绩分析表
平均分 | 方差 | 中位数 | 众数 | 合格率 | 优秀率 | |
男生 | 2 | 8 | 7 | 95% | 40% | |
女生 | 7.92 | 1.99 | 8 | 96% | 36% |
根据以上信息,解答下列问题:
(1)在这次测试中,该班女生得10分的人数为4人,则这个班共有女生人;
(2)补全初二1班男生体育模拟测试成绩统计图,并把相应的数据标注在统计图上;
(3)补全初二1班体育模拟测试成绩分析表;
(4)你认为在这次体育测试中,1班的男生队、女生队哪个表现更突出一些?并写出一条支持你的看法的理由;
(5)体育康老师说,从整体看,1班的体育成绩在合格率方面基本达标,但在优秀率方面还不够理想,因此他希望全班同学继续加强体育锻炼,争取在期末考试中,全班的优秀率达到60%,若男生优秀人数再增加6人,则女生优秀人数再增加多少人才能完成康老师提出的目标?
【题目】已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表,
x | 6.17 | 6.18 | 6.19 | 6.20 |
y | ﹣0.03 | ﹣0.01 | 0.02 | 0.04 |
则方程ax2+bx+c=0的一个解的范围是_____.
