题目内容
抛物线y=-x2+bx+c的部分图象如图所示，若y＞0，则x的取值范围是 ．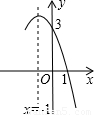
【答案】分析：根据抛物线的对称轴为x=-1，一个交点为（1，0），可推出另一交点为（-3，0），结合图象求出y＞0时，x的范围．
解答：解：根据抛物线的图象可知：
抛物线的对称轴为x=-1，已知一个交点为（1，0），
根据对称性，则另一交点为（-3，0），
所以y＞0时，x的取值范围是-3＜x＜1．
点评：此题的关键是根据二次函数的对称轴与对称性，找出抛物线y=-x2+bx+c的完整图象．
解答：解：根据抛物线的图象可知：
抛物线的对称轴为x=-1，已知一个交点为（1，0），
根据对称性，则另一交点为（-3，0），
所以y＞0时，x的取值范围是-3＜x＜1．
点评：此题的关键是根据二次函数的对称轴与对称性，找出抛物线y=-x2+bx+c的完整图象．
练习册系列答案
相关题目
A是抛物线与x轴的另一个交点．
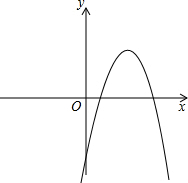已知一元二次方程-x2+bx+c=0的两个实数根是m，4，其中0＜m＜4．
16、已知抛物线y=x2+bx+c的部分图象如图所示，若方程x2+bx+c=0有两个同号的实数根，则c的值可以是