题目内容
(2010•白云区一模)一条不经过第二象限的直线与反比例函数y=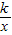 的图象交于点P(3,2),该直线与x轴所夹的锐角为45°.
的图象交于点P(3,2),该直线与x轴所夹的锐角为45°.(1)求反比例函数的解析式;
(2)根据题意,在如图所给的坐标系中画出直线的图象,并求出这条直线的函数解析式;
(3)在图中画出该直线关于y轴对称的图形.
【答案】分析:(1)将P点坐标代入反比例函数的解析式中,即可求得待定系数的值,从而确定该函数的解析式.
(2)已知直线不经过第二象限,那么它的斜率应大于0,又直线与x轴的夹角为45°,即斜率为tan45°=1,然后设出该直线的解析式,将P点坐标代入求解即可.
(3)由于两条直线关于y轴对称,那么它们的斜率互为相反数,与y轴交点不变,即函数解析式中常数项相同.
解答: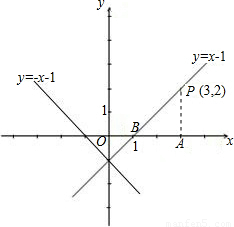 解:(1)∵y=
解:(1)∵y=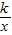 的图象经过点P(3,2),
的图象经过点P(3,2),
把x=3,y=2人代入y=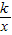 中,(1分)
中,(1分)
∴得2=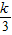 ,即k=6,(2分)
,即k=6,(2分)
∴反比例函数的解析式为:y=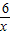 ;(3分)
;(3分)
(2)如图,过点P画与x轴夹角为45°的直线.(5分)
设其与x轴的交点为B.
过P点作PA⊥x轴,垂足为A,
则PA=2,A的坐标为(3,0).(6分)
在Rt△ABP中,∵∠ABP=45°,
∴∠APB=45°,∴AB=AP=2,
OB=OA-AB=3-2=1,
∴点B的坐标为(1,0).(8分)
设直线的解析式为y=kx+b,(9分)
把P(3,2)及B(1,0)的坐标代入y=kx+b,(10分)
解得k=1,b=-1.(11分)
∴这条直线的解析式为:y=x-1.(12分)
(3)如图,直线y=-x-1即为所求.(14分)
点评:此题主要考查了用待定系数法确定函数解析式的方法,以及函数图象的几何变换,难度适中.
(2)已知直线不经过第二象限,那么它的斜率应大于0,又直线与x轴的夹角为45°,即斜率为tan45°=1,然后设出该直线的解析式,将P点坐标代入求解即可.
(3)由于两条直线关于y轴对称,那么它们的斜率互为相反数,与y轴交点不变,即函数解析式中常数项相同.
解答:
 解:(1)∵y=
解:(1)∵y=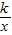 的图象经过点P(3,2),
的图象经过点P(3,2),把x=3,y=2人代入y=
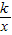 中,(1分)
中,(1分)∴得2=
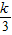 ,即k=6,(2分)
,即k=6,(2分)∴反比例函数的解析式为:y=
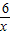 ;(3分)
;(3分)(2)如图,过点P画与x轴夹角为45°的直线.(5分)
设其与x轴的交点为B.
过P点作PA⊥x轴,垂足为A,
则PA=2,A的坐标为(3,0).(6分)
在Rt△ABP中,∵∠ABP=45°,
∴∠APB=45°,∴AB=AP=2,
OB=OA-AB=3-2=1,
∴点B的坐标为(1,0).(8分)
设直线的解析式为y=kx+b,(9分)
把P(3,2)及B(1,0)的坐标代入y=kx+b,(10分)
解得k=1,b=-1.(11分)
∴这条直线的解析式为:y=x-1.(12分)
(3)如图,直线y=-x-1即为所求.(14分)
点评:此题主要考查了用待定系数法确定函数解析式的方法,以及函数图象的几何变换,难度适中.

练习册系列答案
相关题目
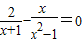 的解是( )
的解是( )
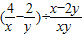 = .
= .