Question

【题目】如图，在平面直角坐标系中，点A在抛物线y=x2﹣2x+2上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为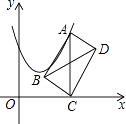

Answer 1

【答案】1
【解析】解：∵y=x2﹣2x+2=（x﹣1）2+1，
∴抛物线的顶点坐标为（1，1），
∵四边形ABCD为矩形，
∴BD=AC，
而AC⊥x轴，
∴AC的长等于点A的纵坐标，
当点A在抛物线的顶点时，点A到x轴的距离最小，最小值为1，
∴对角线BD的最小值为1．
所以答案是1．
【考点精析】关于本题考查的垂线段最短和矩形的性质，需要了解连接直线外一点与直线上各点的所有线段中，垂线段最短；现实生活中开沟引水，牵牛喝水都是“垂线段最短”性质的应用；矩形的四个角都是直角，矩形的对角线相等才能得出正确答案．