题目内容
一个围棋盘由18×18个边长为1的正方形小方格组成，一块边长为1.5的正方形卡片放在棋盘上，被这块卡片覆盖了一部分或全部的小方格共有n个，则n的最大值是（ ）
| A、4 | B、6 | C、10 | D、12 |
分析：要n取最大值，就让边长为1.5的正方形卡片边与小方格的边成一定角度．
解答：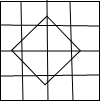
解：∵卡片的边长为1.5，∴卡片的对角线长为2＜
＜3，
且小方格的对角线长
＜1.5．
故该卡片可以按照如图所示放置：
图示为n取最大值的时候，n=12．
故选D．
解：∵卡片的边长为1.5，∴卡片的对角线长为2＜3
| ||
| 2 |
且小方格的对角线长
| 2 |
故该卡片可以按照如图所示放置：
图示为n取最大值的时候，n=12．
故选D．
点评：本题考查的是已知正方形边长正方形对角线长的计算，旋转正方形卡片并且找到合适的位置使得n为最大值，是解题的关键．
练习册系列答案
相关题目