题目内容
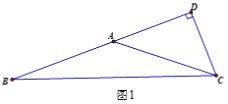
【题目】已知:如图,![]() ABC中,CD⊥BA交BA延长线于点D,∠ABC=∠ACB
ABC中,CD⊥BA交BA延长线于点D,∠ABC=∠ACB
(1)求证:∠DCB=![]() ∠BAC.
∠BAC.
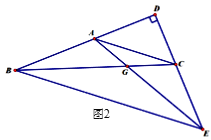
(2)如图2,过点B作BE∥AC交DC延长线于点E,连接AE交BC于点G.若∠DCB=2∠CAE+∠ABC,求证:∠AEB=∠AEC.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据三角形内角和的性质,结合题意即可解答.
(2)根据平行线的性质,再结合题意即可得出答案.
解:(1)∵∠ABC=∠ACB
∴∠DAC=2∠B
∴∠BAC=180°-2∠B
∵∠D=90°
∴∠DCB=90°-∠DAC+∠ACB=90°-∠B.
∴∠BAC=2∠BCD.
(2)∵∠DCB=∠ACB+∠ACD=2∠CAE+∠CBE
∴∠ACD=2∠CAE
∵AC//BE
∴∠CAE=∠AEB
∴∠AEB=∠AEC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目