题目内容
 如图,点P为等边△ABC的边AB上一点,Q为BC延长线上一点,AP=CQ,PQ交AC于D,
如图,点P为等边△ABC的边AB上一点,Q为BC延长线上一点,AP=CQ,PQ交AC于D,(1)求证:DP=DQ;
(2)过P作PE⊥AC于E,若BC=4,求DE的长.
分析:(1)过点P作PM∥BC,根据两直线平行,内错角相等可得∠DPM=∠Q,判断出△APM是等边三角形,根据等边三角形的性质可得AP=PM,然后求出PM=CQ,再利用“角角边”证明△DPM和△DQC全等,根据全等三角形对应边相等证明即可;
(2)根据全等三角形对应边相等可得DM=DC,根据等腰三角形三线合一的性质可得AE=EM,然后求出DE=
AC,代入数据进行计算即可得解.
(2)根据全等三角形对应边相等可得DM=DC,根据等腰三角形三线合一的性质可得AE=EM,然后求出DE=
| 1 |
| 2 |
解答: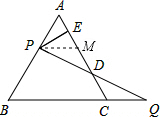 (1)证明:如图,过点P作PM∥BC,则∠DPM=∠Q,
(1)证明:如图,过点P作PM∥BC,则∠DPM=∠Q,
∵△ABC为等边三角形,
∴△APM是等边三角形,
∴AP=PM,
又∵AP=CQ,
∴PM=CQ,
在△DPM和△DQC中,
,
∴△DPM≌△DQC(AAS),
∴DP=DQ;
(2)∵△DPM≌△DQC,
∴DM=DC,
∵PE⊥AC,△APM是等边三角形,
∴AE=EM,
∴DE=DM+EM=
AC,
∵等边三角形ABC的边BC=4,
∴AC=4,
∴DE=
×4=2.
 (1)证明:如图,过点P作PM∥BC,则∠DPM=∠Q,
(1)证明:如图,过点P作PM∥BC,则∠DPM=∠Q,∵△ABC为等边三角形,
∴△APM是等边三角形,
∴AP=PM,
又∵AP=CQ,
∴PM=CQ,
在△DPM和△DQC中,
|
∴△DPM≌△DQC(AAS),
∴DP=DQ;
(2)∵△DPM≌△DQC,
∴DM=DC,
∵PE⊥AC,△APM是等边三角形,
∴AE=EM,
∴DE=DM+EM=
| 1 |
| 2 |
∵等边三角形ABC的边BC=4,
∴AC=4,
∴DE=
| 1 |
| 2 |
点评:本题考查了等边三角形的性质,全等三角形的判定与性质,等腰三角形三线合一的性质,作辅助线构造出等边三角形和全等三角形是解题的关键,也是本题的难点.

练习册系列答案
相关题目
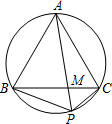 如图,点P为等边△ABC外接圆劣弧BC上一点.
如图,点P为等边△ABC外接圆劣弧BC上一点.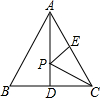 如图,点E为等边△ABC中AC边的中点,AD⊥BC,且AD=5,P为AD上的动点,则PE+PC的最小值为
如图,点E为等边△ABC中AC边的中点,AD⊥BC,且AD=5,P为AD上的动点,则PE+PC的最小值为