Question

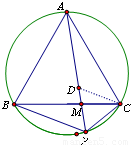
（2011四川泸州，26，7分）如图，点P为等边△ABC外接圆劣弧BC上一点．

（1）求∠BPC的度数；

（2）求证：PA=PB+PC；

（3）设PA，BC交于点M，若AB=4，PC=2，求CM的长度．

 

 

Answer 1

【答案】

解：（1）∵△ABC为等边三角形，∴∠BAC=60°，

∵点P为等边△ABC外接圆劣弧BC上一点，∴∠BPC+∠BAC=180°，∴∠BPC=120°，

（2）在PA上截取PD=PC，

∵AB=AC=BC，∴∠APB=∠APC=60°，∴△PCD为等边三角形，∴∠ADC=120°，

∴△ACD≌△BCP，∴AD=PB，∴PA=PB+PC；

（3）∵△CDM∽△ACM，∴CM：AM=DM：MC=DC：AC=2：4=1：2，

设DM=x，则CM=2x，BM=4-2x，PM=2-x，AM=4x，∵△BPM∽△ACM，∴BP：AC=PM：CM，

即3x：4=（2-x）：2x，解得，x=（舍去负号），则x=，∴CM= ．

 

【解析】略